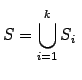

Next: Ejemplos
Up: Fractales autosemejantes
Previous: Fractales autosemejantes
Los fractales autosemejantes, son aquellos que tienen la propiedad de que el
fractal puede descomponerse en copias a escala de él mismo.
Esto nos lleva a trabajar con conjuntos autosemejantes, para designar a todo
subconjunto
tal que:
- S es cerrado y acotado (contiene a todos sus puntos de la frontera y
puede inscribirse en una circunferencia)
- S se expresa :
con cada
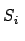 semejante a S con la misma razón de semjanza r
<1 (homotecia de contracción
semejante a S con la misma razón de semjanza r
<1 (homotecia de contracción 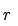 ) tal que los conjuntos
) tal que los conjuntos
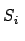 no
se solapen, es decir
no
se solapen, es decir
Para generar fractales se usa el siguiente teorema (que no demuestro, porque
está en los libros de la bibliografía)
Theorem
Sea
una semejanza con razón r y sea
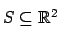 un subconjunto
cerrado y acotado. Entonces
un subconjunto
cerrado y acotado. Entonces
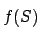 es semejante a S es decir es una copia
a escala r, que ha sido rotada y trasladada de su posición original
es semejante a S es decir es una copia
a escala r, que ha sido rotada y trasladada de su posición original
Pantaleón David Romero Sánchez
2002-12-12