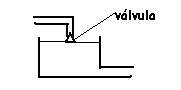
- Siglo XIV: Clepsidra de Herón de Alejandría, solucionaba el caudal que llegaba a un tanque con un sencillo sistema de control basado en una válvula:
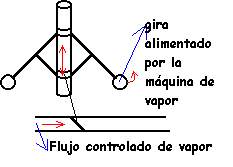
-1788: regulador de velocidad centrífugo de James Watt, primer trabajo significativo en el control automático.
-1922: Minorsky trabajó en los controladores automáticos para dirigir embarcaciones y demostro que la estabilidad puede determinarse a partir de las ecuaciones diferenciales que describen un sistema.
-1932: Nyquist diseño un procedimiento para determinar la estabilidad en lazo cerrado, con base a la respuesta en lazo abierto cuando la entrada es una senoidal.
-1934: Introdujo el término servomecanismo para los sistemas de posición y los analizó.
-Década de los 40: Los métodos de respuesta en frecuencia se hicieron muy importantes entre los ingenieros para diseñar sistemas de control lineales.
-Final de los 40, principio de los 50: Desarrollado por completo el método del lugar de las raices propuesto por Evans.
-Desde principio de los 50: sistemas optimos de control.
-Desde los 60: Puesto que los computadores lo permiten se pueden estudiar a fondo los sistemas complejos en el dominio del tiempo, estos sistemas estan formados por múltiples entradas y múltiples salidas lo cual trae consigo un gran número de ecuaciones que los métodos tradicionales no pueden dar solución eficientemente. Para dar respuesta a estos sistemas se ha desarrollado la teoria de control moderna que conforme la tecnología lo ha permitido ha avanzado significativamente hasta estas fechas.
Referencias:
- f(t) = una función del tiempo t / f(t) = 0 para t< 0.
- s = variable compleja(es por ello que si de complejos vas un poco perdid@ te recomiendo que les des un repaso).
- £ = indica que la función que le sigue se va a transformar mediante Laplace.
- F(s) = transformada de Laplace de f(t).
La transformada de laplace se obtiene:
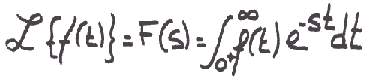
Ej: Sea x(t) = t
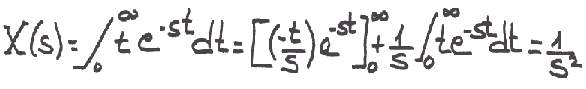
Vemos que a partir de la función x(t) = t obtenemos X(s)= 1/s2 en el plano complejo.
A simple vista la pregunta es, ¿para que hacer este cálculo con integrales cuando suele ser difícil?
La respuesta reside en la simplificación del análisis de los sistemas de control.
La modelización de un sistema de control consiste en obtener las ecuaciones que lo caracterizan, es el primer paso necesario para poder analizarlo y con ello poder determinar su comportamiento futuro. Estas ecuaciones suelen ser diferenciales, con lo que incluyen derivadas de distintos ordenes sumadas y que implican un serio problema en el futuro análisis. Establecer una metodología que permita determinar la respuesta de los sistemas de control a partir de sus ecuaciones diferenciales es un trabajo muy complejo, pero que la tranformada de fourier ha sido capaz de solventar. La razón a tal ayuda es la característica de simplificar una derivada de orden n en un solo producto:
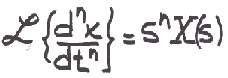
que es mucho más fácil de analizar. Además, cada vez que se presenta una ecuación diferencial no hay que realizar la integral sino que existen unas tablas que simplifican la tarea, haciendo este trabajo casi automático obteniendo un polinomio de números complejos.
Referencias:
- "Se define control como el conjunto de procedimientos que aplicamos para
que un sistema, desde un estado inicial, alcance cierto estado final y se
mantenga en el o muy próximo, independientemente de los cambios en magnitudes
externas o internas que puedan afectar."
- El control de un sistema puede tener 2 finalidades distintas:
- Regulación: consiste en mantener la salida constante independientemente
de la variación de magnitudes externas.
ej: Mantener constante la orientación de una antena a un satélite. - Seguimiento de trayectorias:hacer que la variable de salida tenga
en todo momento un valor tan próximo como sea posible al de alguna
variable de entrada.
ej: Controlar un robot móvil para que siga un camino establecido.
- Regulación: consiste en mantener la salida constante independientemente
de la variación de magnitudes externas.