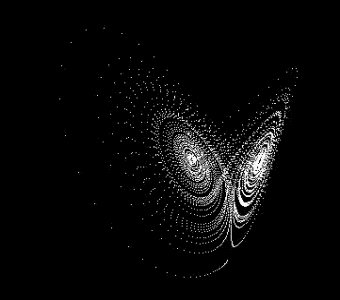
THE LORENZ ATRACTOR:
This is the famous Lorenz atractor, with two singular elliptical points in the phasic space, one very close to the other. Such a small distance between elliptical points makes this atractor to have a chaotic behavior for certain values of its defining parameters. It is very easy to generate the Lorenz atractor in KinetiK. And it is also amazing to animate it and see how it is drawn in 3D (and see it with R-B glasses thanks to the stereographic-projection feature) from any point in space. You can also change the formulae that define the atractor and create your own "Lorenz" atractors.
There are many other examples of systems with chaotic behavior in the KinetiK help file.

BIFURCATION DIAGRAM:
The bifurcation diagram of the Logistic Application can also be generated with KinetiK in a very easy way. In addition, you will be able to alter, at your pleasure, the defining formula of the application, and to verify right away how it affects the bifurcation structure.
You will also be able to simulate all the recurrence laws that cross your mind, simulating the evolution of bacteria populations, victim-predator systems, etc. There are some formulas of other models of population evolution in the help file, so you will be able to experience and play with them using KinetiK.

STRANGE ATRACTOR:
This is the strange atractor corresponding to a cushioned pendulum externally forced to a nonlinear regime using a harmonic force. You can alter the nature of the impelling force of the system with KinetiK, or change the law of friction that cushions the pendulum. KinetiK can draw lots of strange atractors, but can also draw the evolution of the penduli through time in their phasic space, dancing crazy through the screen without any defined pattern when we find the right force that puts them into chaotic regime.
In the help file, I try to explain a little bit what the strange atractors are and how can they be drawn with KinetiK.

RELATIVISTIC PRECESSION:
You can also simulate the gravitational attraction generated by the Schwartzschild metric (solution of the Einstein equations of General Relativity for a point-like mass distribution) in the low-velocity regime. Thanks to KinetiK, you will be able to compare a relativistic orbit with its Newtonian equivalent in conditions of very intense gravitational fields. You will see how, 'magically', General Relativity predicts a precession effect that the Theory of Universal Gravitation of Newton does not contemplate.
With KinetiK, you will be able to play with both, General Relativity and Special Relativity. In the help file, I include some other examples with which you will have fun enjoying with the beauty that surrounds these theories on the structure of space and time.
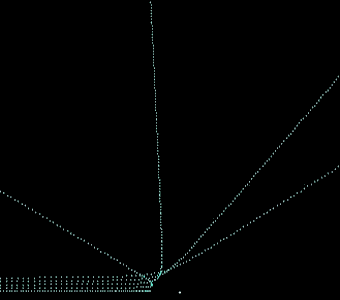
RUTHERFORD DISPERSION:
You can also simulate scattering experiments with KinetiK, with electron screening and with naked nuclei. You can play with lots of possibilities, like trying to measure the radius of the nucleus from the scattering distribution by increasing the energy of the incident particles, just as it is done in real life!

WAVES IN ELASTIC MEDIA:
With KinteiK, you can simulate atomic networks and generate longitudinal waves, cross-sectional waves, or a combinacion of both. It can be very didactic to measure the frequencies of both types of waves, in order to deduce which one has a greater speed in the elastic medium. You can also generate anisotropic forces in the network and even 2D networks, add gravity or friction to them, etc. An absolute control of the simulated physical system is taken with KinetiK.
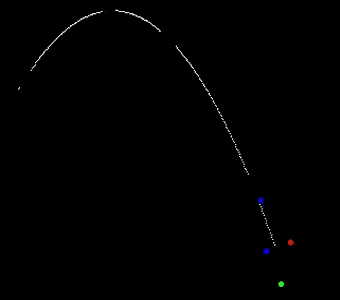
PARTICLE SYSTEMS:
There are lots of examples with which you can strength your knowledge on particle system dynamics using KinetiK. The attached figure shows the evolution of four bodies joined with wharves among them, and put under the action of gravity. KinetiK has drawn the trajectory of the Centre of Mass in white color. As we can see, the Center of Mass describes a perfect parabola, which makes us conclude that the presence of wharves is not affecting its trajectory.
But what would happen if suddenly, during the flight of the bodies, one of the wharves is broken or its elastic constant is changed? How would it affect the trajectory of the Centre of Masses? KinetiK can give you the answer very easily, since, even without stopping the animation, you can alter "in real time" any of the variables of the system.