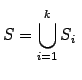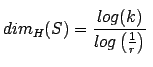Triángulo de Sierspinski

Si observamos por el ejemplo en la figura 2.3 (a) observamos que el triángulo de Sierspinski se descompone en 3 copias a escala de él mismo. Para ello, llamamos

$$T\subseteq \mathbb{R}^{2}$$

al triángulo de Sierspinski y

$$T_{1},T_{2},T_{3}$$

los tres triángulos en que se descompone T:

$$T=\bigcup _{i=1}^{3}T_{i}$$

las 3 semejanzas

$$f_{i},\, \, i=1,2,3$$

de modo que

$$f_{i}(T)=T_{i}\, \, \, i=1,2,3$$

son las siguientes:

$$\begin{array}{c} f_{1}(a_{1},a_{2})=\underbrace{\frac{1}{3}\... ...0 \end{array}\right) }_{Traslaci\acute{o}n}\\ \par \end{array}$$

mediante las cuales se T se descompone como:

$$T=\bigcup ^{3}_{i=1}f_{i}(T)$$

Notar que esto requiere «mucha visualización». Esto es complejo en sí, la visualización es algo que se debe estimular pero también depende de la capacidad de cada cuál en darse cuenta de lo que tiene delante.

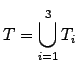
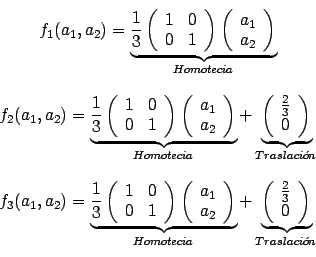
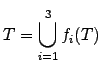
Pero pese a lo fácil que parece la definción de «fractal» (=dimensión fraccionaria) no es fácil determinar su dimensión. Hay que recurrir a la dimensión de Hausdorff. Ahí va la definción de dimensión de Hausdorff:

Definition 4.1   La dimensión de Hausdorff de un conjunto autosemejante

$$S=\bigcup _{i=1}^{k}S_{i}$$

donde cada

$$S_{i}\, \, i=1,\ldots ,k$$

es semejante a con una misma razón de semejanza r < 1 se define como

$$dim_{H}(S)=\frac{log(k)}{log\left( \frac{1}{r}\right) }$$

siendo

$$\begin{array}{c} k=n\acute{u}mero\, \, de\, \, copias\, \, e... ...{1}{r}=raz\acute{o}n\, \, de\, \, la\, \, Homotecia \end{array}$$

¿Porqué recurrir a la dimensión de Hausdorff? porque es la que mejor aproxima la dimensión del fractal.