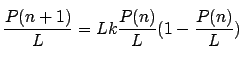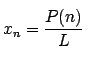

Next: Fractales y Caos
Up: Aplicaciones
Previous: Aplicaciones
Se usa el término sistema dinámico, para aludir a situaciones
que se encuentran en permante evolución. Los fractales son muy útiles en el
estudio de tales sistemas, no sólo porque permiten modelizar la situación real,
sino también porque permiten hacer predicciones sobre el estado de un sistema,
cuando evoluciona el tiempo.
Un sistema dinámico discreto (nos permiten discretizar una ecuación diferencial
y estudiar la evolución de sus soluciones en términos de su estabilidad) es
un sistema de variables que evolución en el tiempo de modo que el estado del
sistema en el instante k+1 puede conocerse a partir del instante k,
a través de ecuación de iteración:
de modo que a partir de un valor inicial
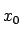 comocemos el estado del
sistema en el instante k.
El ejemoplo más significativo de sistemas dinámicos es, la dinámica de poblaciones.
El más conocido es el modelo de Robert May formulado en 1976 para el estudio
de una población de insectos, en el que daba una relación entre dos poblaciones
del mismo tipo de insecto, en años consecutivos:
siendo
la población en el año n y L la población máxima. Si renormalizamos
el modelo:
que se transforma en
con
que podemos considerar entre 0 y 1. Cuando hablamos del crecimiento de la población
hablamos también del la red de absteciminento de aguas, para
prever dentro de lo posible cómo afectará al suministro el crecimiento de población.
Este estudio se aplica a redes de aguas residuales o construcción
de depuradoras.
comocemos el estado del
sistema en el instante k.
El ejemoplo más significativo de sistemas dinámicos es, la dinámica de poblaciones.
El más conocido es el modelo de Robert May formulado en 1976 para el estudio
de una población de insectos, en el que daba una relación entre dos poblaciones
del mismo tipo de insecto, en años consecutivos:
siendo
la población en el año n y L la población máxima. Si renormalizamos
el modelo:
que se transforma en
con
que podemos considerar entre 0 y 1. Cuando hablamos del crecimiento de la población
hablamos también del la red de absteciminento de aguas, para
prever dentro de lo posible cómo afectará al suministro el crecimiento de población.
Este estudio se aplica a redes de aguas residuales o construcción
de depuradoras.


Next: Fractales y Caos
Up: Aplicaciones
Previous: Aplicaciones
Pantaleón David Romero Sánchez
2002-12-12