

Next: La curva de Kock
Up: Definición intuituva de Fractal
Previous: Definición intuituva de Fractal
Es un ejemplo de conjunto infinito pero que su medida topológica es igual a
0.
CONSTRUCCIÓN
- Consideramos el intervalo unidad I=[0,1]
al que dividimos en 3 partes iguales y quitamos el tercio central. Luego nos
queda
cada uno de ellos de longitud
- Los intervalos
a su vez se dividen en 3 intervalos, siguiendo el proceso dado en 1. Por tanto
nos quedamos con:
ahora cada uno es de longitud
- Si repetimos este proceso, en la etapa k-ésima habremos obtenido
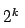 intervalos cerrados
cada uno de ellos de longitud
intervalos cerrados
cada uno de ellos de longitud
Este proceso nos permite dar la definición de conjunto de Cantor. Si llamamos
los conjuntos forman una sucesión decreciente
Por tanto el CONJUNTO DE CANTOR se define:
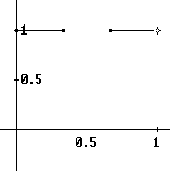
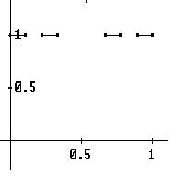
Podemos ver los procesos de construcción del conjunto de Cantor de manera visual,
cómo sigue
Figure 2.1:
Diferentes procesos de construcción del fractal de Cantor. (a) tenemos
el primer paso de construcción en (b) el segundo y en (c) el tercero
(a)
 (b)
(c)
|


Next: La curva de Kock
Up: Definición intuituva de Fractal
Previous: Definición intuituva de Fractal
Pantaleón David Romero Sánchez
2002-12-12
![$\displaystyle I_{11}=\left[ 0,\frac{1}{3}\right] \, \, \, I_{12}=\left[ \frac{2}{3},1\right] $](img5.gif)
![$\displaystyle \frac{1}{3}(longitud\, \, de\, \, [a,b])=\frac{1}{3}(b-a)$](img6.gif)
![$\displaystyle I_{21}=\left[ 0,\frac{1}{9}\right] ,I_{22}=\left[ \frac{2}{9},\fr...
...{23}=\left[ \frac{2}{3},\frac{7}{9}\right] ,I_{24}=\left[ \frac{8}{9},1\right] $](img8.gif)
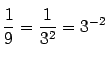
![$\displaystyle I_{11}=\left[ 0,\frac{1}{3}\right] \, \, \, I_{12}=\left[ \frac{2}{3},1\right] $](img5.gif)
![$\displaystyle \frac{1}{3}(longitud\, \, de\, \, [a,b])=\frac{1}{3}(b-a)$](img6.gif)
![$\displaystyle I_{21}=\left[ 0,\frac{1}{9}\right] ,I_{22}=\left[ \frac{2}{9},\fr...
...{23}=\left[ \frac{2}{3},\frac{7}{9}\right] ,I_{24}=\left[ \frac{8}{9},1\right] $](img8.gif)
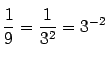
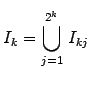
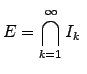
 (b)
(b)

