La curva de Kock

Descubierta por el matemático Helge Von Koch en 1904. Veamos cómo se construye

1. Partimos el segmento unidad, [0,1] en 3 partes iguales.
2. Sustituimos la parte central por dos segmentos que junto con dicha parte, formarán un triángulo rectángulo
3. Repetir los pasos 1,2 con los segmentos restantes

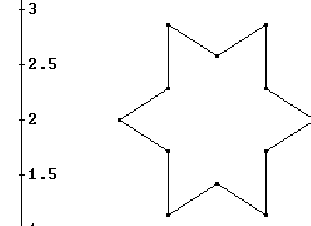
Veamos visualmente el fractal en una de las etapas de la construcción

Figure 2.2: Fractal de Kock

Si se observa la figura se verán una especie de cuadrados. Éstos nos dan una visión de la «geometría del fractal». Es decir, podemos generar el fractal de otra manera. A base de aplicaciones contractivas: homotecias, traslaciones y rotaciones.

Note 2.1   Veremos en la sección de fractales semejantes el significado de estos cuadrados cuál es.

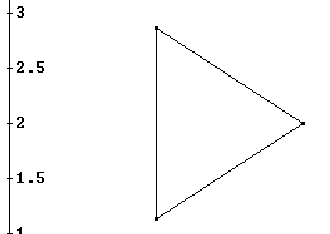
Como consecuencia de la construcción anterior tenemos la isla de Koch. Se procede igual que en los pasos 1,2,3 pero en lugar de partir un segmento lo hacemos sobre los lados de un triángulo equilátero, que mide (cada lado) 1 cm. Así tenemos el fractal (figura 2.3)

Figure 2.3: Proceso de construcción de la ISLA DE KOCH