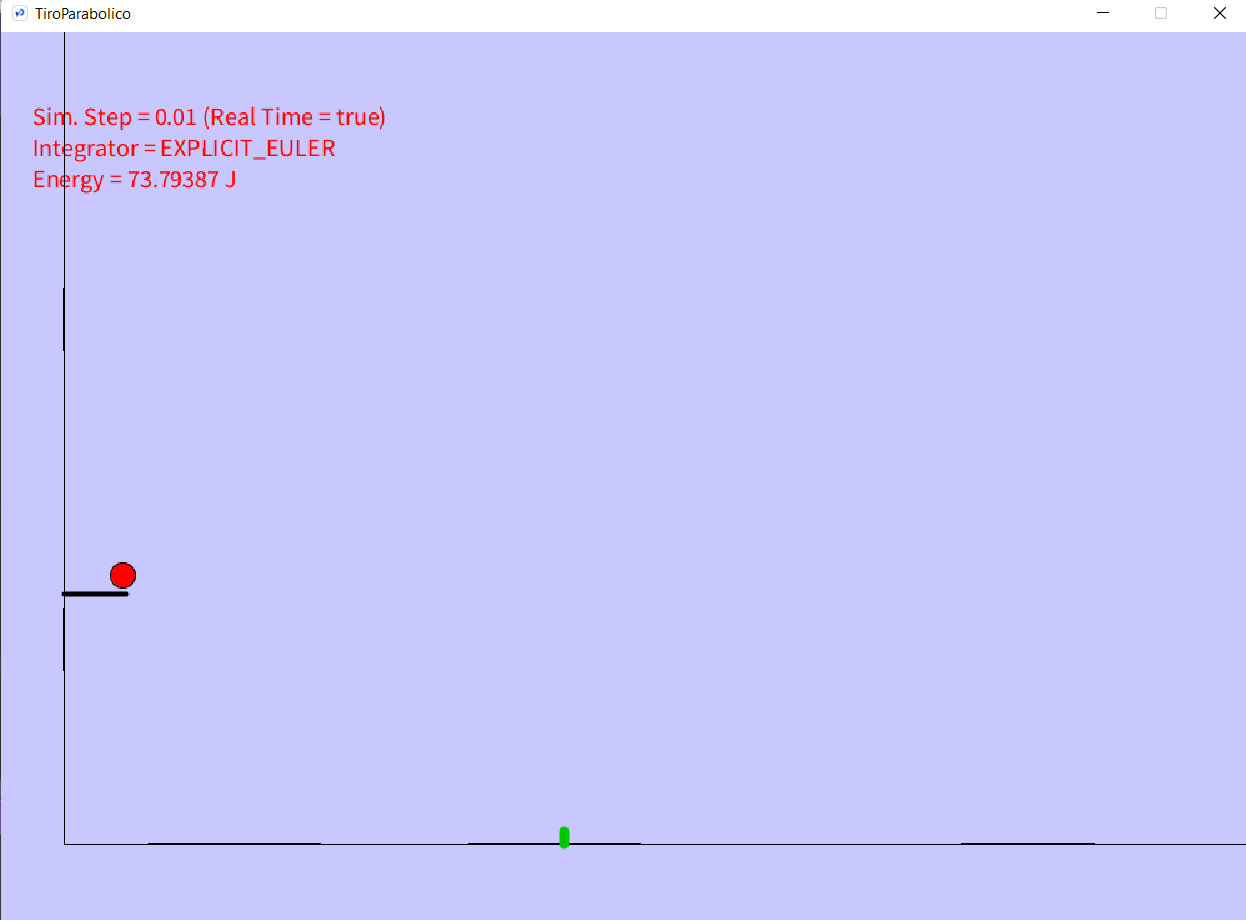
Montaña Rusa
Descripción de la simulación:
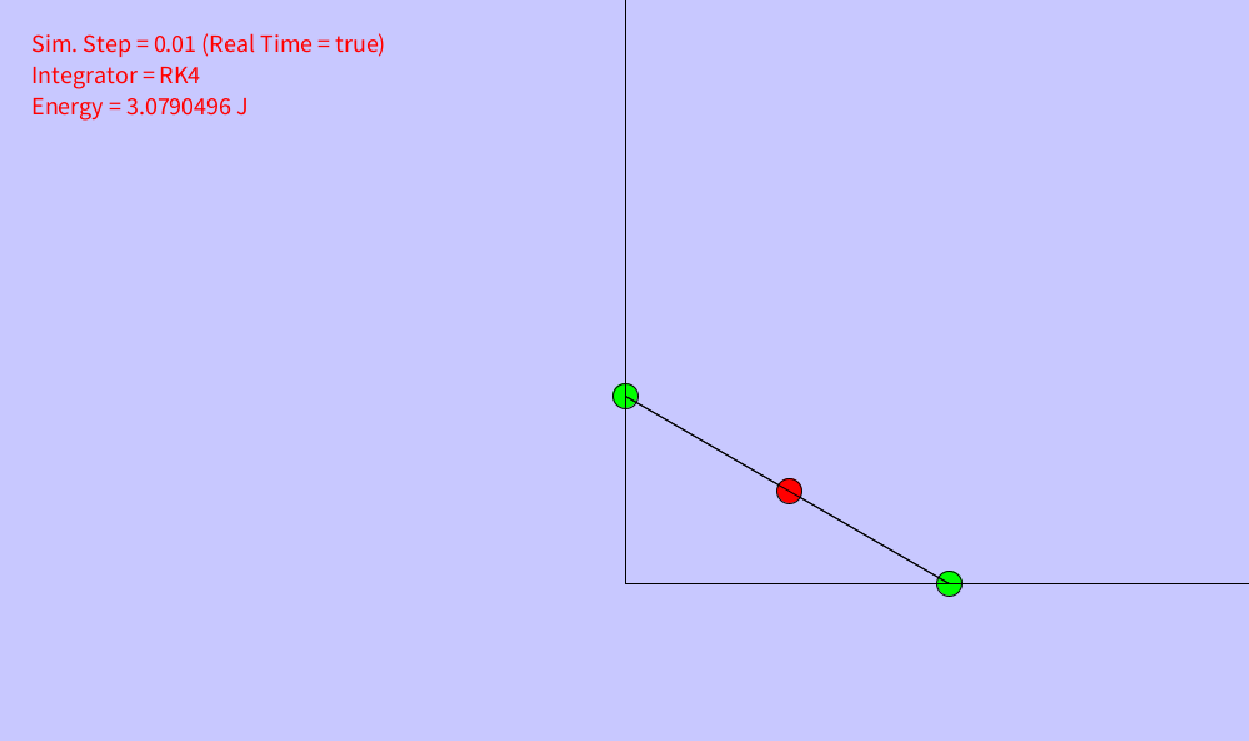
Como primer trabajo en Processing dibujamos un recorrido cualquiera, por el cual debía circular una pelota.
Cada tramo queda representado por un color diferente. La bola sufre acelereación en los tramos descendentes
y mantiene una velocidad constante en los ascendentes
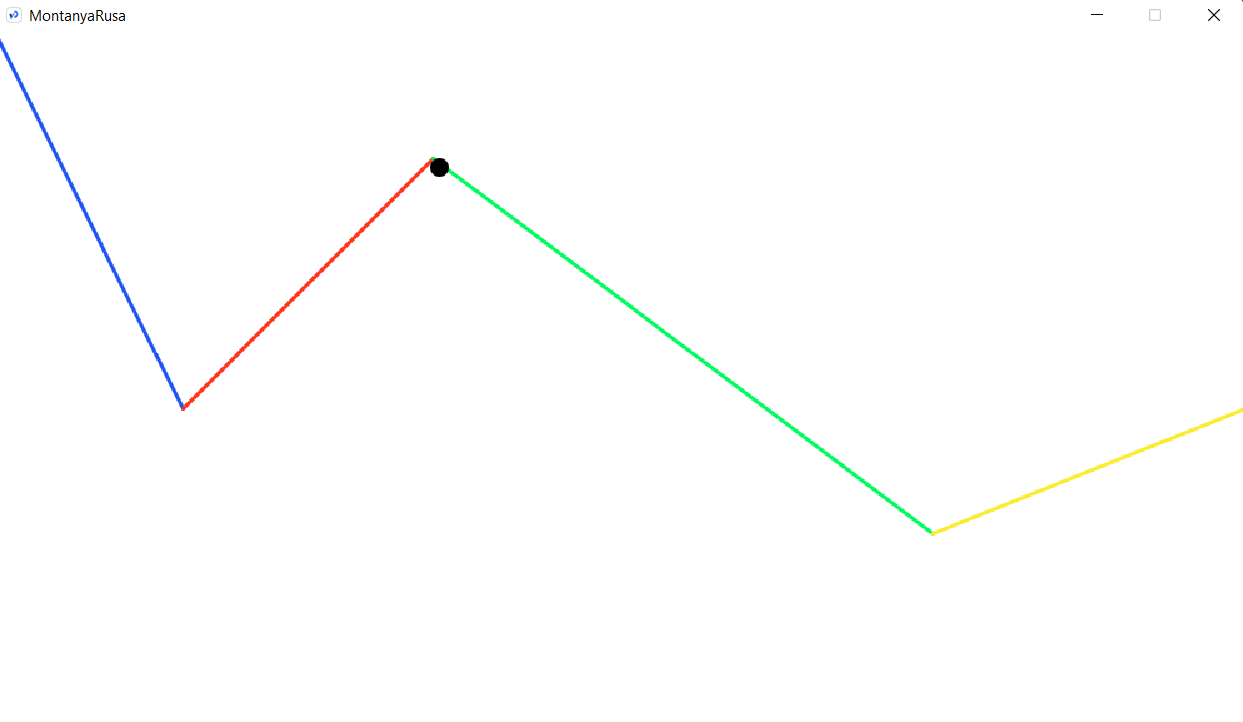
Como primer trabajo en Processing dibujamos un recorrido cualquiera, por el cual debía circular una pelota.
Cada tramo queda representado por un color diferente. La bola sufre acelereación en los tramos descendentes
y mantiene una velocidad constante en los ascendentes