Next: VLBI con sonido Up: LA INTERFEROMETRÍA EN RADIOASTRONOMÍA Previous: Ajuste de Franjas (Fringe
Los radiotelescopios son, con diferencia, los instrumentos más sensibles del mundo. Si sumaramos el flujo que todas las antenas de VLBI han conseguido correlacionar desde que empezaron a tomar datos, la energía total recolectada no sería suficiente ni para incrementar la temperatura de una gota de agua en una milésima de grado.
En este apartado trataremos de describir el proceso con el que se consiguen calibrar las amplitudes de las extremadamente débiles señales que son captadas por los radiotelescopios.
La unidad típica de densidad de flujo en radioastronomía recibe el nombre
de Jansky
(Jy), en honor a Karl Jansky, ingeniero americano hoy considerado padre de la
radioastronomía. Un Jansky equivale a 10![]() W m
W m![]() Hz
Hz![]() .
.
Esto es, el Jansky se refiere a una potencia por unidad de superficie (es decir, un flujo) por unidad de frecuencia, lo que hace que sea una densidad de flujo, donde la palabra ``densidad'' hace referencia a ``por unidad de frecuencia''.
El orden de magnitud de esta unidad de flujo en Radioastronomía ya habla por sí solo en cuanto a la cantidad de energía captada y correlacionada se refiere.
Pasemos ahora a hablar un poco sobre cómo se consiguen calibrar las amplitudes de las visibilidades del interferómetro, una vez hemos hablado ya largo y tendido sobre las fases.
En la práctica, el calibrado de las amplitudes se suele efectuar antes del Fringe Fitting, de manera que el ajuste de las correcciones de las antenas se haga atribuyendo a la visibilidad de cada línea de base el peso estadístico que merece.
Calibrar en amplitudes no es más que multiplicar todas las visibilidades por unos números reales que convierten una amplitud de coeficiente de correlación (sin unidades) en una densidad de flujo (en Jy).
Para explicar el proceso de calibración de amplitudes necesitamos definir primero algunas magnitudes de interés, como son la Temperatura de Sistema y de Antena.
Sea ![]() la potencia que entra en el receptor de una antena proveniente
de la fuente
la potencia que entra en el receptor de una antena proveniente
de la fuente ![]() , que podría ser desde la fuente celeste a
estudiar hasta cualquier emisor de ruido en la electrónica de la estación.
, que podría ser desde la fuente celeste a
estudiar hasta cualquier emisor de ruido en la electrónica de la estación.
Definimos como Temperatura Equivalente, a la temperatura ![]() que
obedece a la ecuación:
que
obedece a la ecuación:
donde ![]() es la potencia recibida,
es la potencia recibida, ![]() es la constante de Boltzmann,
es la constante de Boltzmann, ![]() es
la ganancia del amplificador de voltaje del receptor y
es
la ganancia del amplificador de voltaje del receptor y ![]() es la
anchura de banda a la que observamos. Esto es, la temperatura
equivalente a la potencia
es la
anchura de banda a la que observamos. Esto es, la temperatura
equivalente a la potencia ![]() es aquella que, de acuerdo a la
ecuación de Boltzmann, produciría un cuerpo negro a dicha temperatura,
amplificando su potencia por el factor
es aquella que, de acuerdo a la
ecuación de Boltzmann, produciría un cuerpo negro a dicha temperatura,
amplificando su potencia por el factor ![]() .
.
A partir de esta sencilla definición podemos hablar, pues, de la
Temperatura de Sistema (![]() ) como la equivalente a la
potencia generada por todo el ruido de amplificadores y receptores en cada
estación. Esta temperatura, pues, representa la mayor parte de la señal que
es ajena a la fuente en estudio. En VLBI, no obstante, la Temperatura de
Sistema que se suele usar es la llamada on source que, como su propio
nombre indica, es la equivalente a la registrada por la antena cuando también
se observa la fuente. Dado que las fuentes producen en las antenas una señal
mucho menor que el ruido de la electrónica, la diferencia entre ambas
temperaturas es a efectos prácticos despreciable4.
) como la equivalente a la
potencia generada por todo el ruido de amplificadores y receptores en cada
estación. Esta temperatura, pues, representa la mayor parte de la señal que
es ajena a la fuente en estudio. En VLBI, no obstante, la Temperatura de
Sistema que se suele usar es la llamada on source que, como su propio
nombre indica, es la equivalente a la registrada por la antena cuando también
se observa la fuente. Dado que las fuentes producen en las antenas una señal
mucho menor que el ruido de la electrónica, la diferencia entre ambas
temperaturas es a efectos prácticos despreciable4.
Por su parte, la llamada Temperatura de Antena (![]() ) es la
equivalente a la potencia generada por el flujo que llega de la fuente
observada. Esta temperatura suele ser del orden de la fracción de Kelvin
(para fuentes con brillos del orden del Jy), mientras que la Temperatura de
Sistema de un buen receptor es del orden de unas pocas decenas de Kelvin.
) es la
equivalente a la potencia generada por el flujo que llega de la fuente
observada. Esta temperatura suele ser del orden de la fracción de Kelvin
(para fuentes con brillos del orden del Jy), mientras que la Temperatura de
Sistema de un buen receptor es del orden de unas pocas decenas de Kelvin.
La sensitividad viene determinada por la relación entre
un flujo entrante en la antena (en Jy) y la temperatura equivalente generada
(en Kelvin). Matemáticamente, la sensitividad ![]() es igual a:
es igual a:
donde ![]() es el flujo de la fuente observada (en
es el flujo de la fuente observada (en ![]() ) y
) y ![]() es la
correspondiente Temperatura de Antena (en
es la
correspondiente Temperatura de Antena (en ![]() ). Como es obvio, una mayor
sensitividad se traduce en un mayor efecto de una fuente sobre la
temperatura equivalente total del receptor, ya que la temperatura de antena
es proporcional a
). Como es obvio, una mayor
sensitividad se traduce en un mayor efecto de una fuente sobre la
temperatura equivalente total del receptor, ya que la temperatura de antena
es proporcional a ![]() .
.
La sensitividad de un radiotelescopio depende de bastantes de factores,
desde atmosféricos hasta de precisión en la construcción de su superficie.
En la práctica, la parte de la sensitividad que depende de la
construcción de cada antena se calcula por interpolación polinómica,
tomando como variable la elevación de apuntado. La parte atmosférica se
estima a partir de medidas de temperatura y humedad relativa durante las
observaciones. Típicamente, ![]() suele valer
suele valer ![]() para las antenas
de VLBA, aunque puede haber valores mucho mayores; el gran radiotelescopio de
Arecibo es capaz de trabajar incluso con sensitividades de
para las antenas
de VLBA, aunque puede haber valores mucho mayores; el gran radiotelescopio de
Arecibo es capaz de trabajar incluso con sensitividades de ![]() .
.
Si ahora multiplicamos la Temperatura de Sistema de una antena por la inversa
de su sensitividad, calcularemos lo que se conoce como Densidad de Flujo
Equivalente del Sistema (System Equivalent Flux Density, ó ![]() ):
):
El ![]() tiene un significado físico sencillo. Simplemente, es el paso a Janskies
de la temperatura total a la que se encuentra el receptor de la antena. Es decir, es
la medida, en unidades de densidad de flujo, del ruido del sistema más
la señal proveniente de la fuente observada.
tiene un significado físico sencillo. Simplemente, es el paso a Janskies
de la temperatura total a la que se encuentra el receptor de la antena. Es decir, es
la medida, en unidades de densidad de flujo, del ruido del sistema más
la señal proveniente de la fuente observada.
Llegados a este punto no nos será muy difícil aceptar que la proporcionalidad entre los coeficientes de correlación (para un par de antenas (i,j)) y la amplitud de las visibilidades correspondientes viene determinada por la expresión:
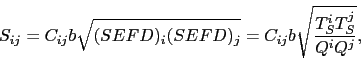 |
(14) |
donde ![]() es la visibilidad calibrada a partir del coeficiente de
correlación
es la visibilidad calibrada a partir del coeficiente de
correlación ![]() ,
, ![]() es la Temperatura de Sistema registrada
por la antena
es la Temperatura de Sistema registrada
por la antena ![]() en el instante que se está calibrando y donde
en el instante que se está calibrando y donde
![]() es la sensitividad de dicha antena.
es la sensitividad de dicha antena.
![]() será, por lo tanto, la Densidad de Flujo Equivalente del Sistema
para la antena
será, por lo tanto, la Densidad de Flujo Equivalente del Sistema
para la antena ![]() . Es decir, su raíz cuadrada será la que deberá
escalar la amplitud (que no potencia) de la señal de la antena
. Es decir, su raíz cuadrada será la que deberá
escalar la amplitud (que no potencia) de la señal de la antena ![]() .
.
No olvidemos que el correlador ha de trabajar con la suma de señal más
ruido, por lo que el escalado de los coeficientes de correlación debe
hacerse según las ![]() (las cuales miden, precisamente, el flujo
equivalente de señal más ruido). La amplitud de los coeficientes de
correlación (típicamente mucho menores que la unidad) será, entonces, la
que dará cuenta de la parte de la
(las cuales miden, precisamente, el flujo
equivalente de señal más ruido). La amplitud de los coeficientes de
correlación (típicamente mucho menores que la unidad) será, entonces, la
que dará cuenta de la parte de la ![]() que corresponde al flujo de la
fuente, dado que el ruido de las antenas no correlacionará, desapareciendo
de la amplitud del coeficiente
que corresponde al flujo de la
fuente, dado que el ruido de las antenas no correlacionará, desapareciendo
de la amplitud del coeficiente ![]() .
.
El factor ![]() tiene en cuenta varias correcciones necesarias de aplicar,
como son las pérdidas en la correlación debidas a la
digitalización de la amplitud de las señales (a 1 ó 2 bits, generalmente),
así como pequeñas correcciones específicas de la estructura interna del
correlador.
tiene en cuenta varias correcciones necesarias de aplicar,
como son las pérdidas en la correlación debidas a la
digitalización de la amplitud de las señales (a 1 ó 2 bits, generalmente),
así como pequeñas correcciones específicas de la estructura interna del
correlador.
La calibración en base a las Temperaturas de Sistema es la propia de la práctica totalidad de estaciones de VLBI. Sencillamente, cada estación no tiene más que medir cada cierto tiempo la potencia generada por los receptores de la antena y, a partir de ahí, calcular la temperatura equivalente. Generalmente, el cálculo de la temperatura se realiza por comparación de la potencia generada por los receptores con la potencia generada por un resistor calibrado mantenido a una temperatura bien controlada.
A partir de estas medidas de Temperatura de Sistema y conociendo las curvas de sensitividad de cada antena (como función de la elevación) podremos llegar a calibrar las amplitudes de nuestros datos sin ningún problema ayudándonos de la ecuación 14.
Ivan Marti-Vidal 2010-05-26