VLBI con sonido

Introducción

Para entender mejor el proceso de correlación en VLBI, lo mejor es simular una observación desde el principio, llevando a cabo todos y cada unos de los pasos de análisis, desde que la señal llega a las antenas hasta que que se obtienen las visibilidades.

Puesto que es imposible adquirir dos radiotelescopios y un correlador con un modesto presupuesto, para concederse el capricho de poder hacer interferometría desde cero, vamos a simular observaciones de VLBI, no con ondas de radio, sino con sonido. Las tarjetas de sonido de los ordenadores actuales son muy potentes, pudiendo muestrear una onda sonora con una precisión similar, o superior, a la de la electrónica empleada en VLBI.

El proceso de correlación en VLBI no se ha reproducido de manera 100% exacta, teniendo en cuenta que la potencia de cálculo de un PC normal en nada es comparable a la de un correlador. No obstante, hemos intentado ser lo más fieles posible al proceso de correlación en VLBI.

Toma de datos

El material usado en estos experimentos es asequible para cualquier laboratorio. Simplemente, se necesitan un par de ordenadores con tarjeta de sonido, dos micrófonos multimedia, un altavoz y un reproductor (de cinta o CD, aunque preferiblemente del último). En caso de que no se tengan dos ordenadores a mano, se pueden empalmar sendos micrófonos a un solo "jack", conectando cada micrófono a uno (y sólo uno) de los canales de audio R y L del jack. Si se opta por esta última opción, cabe decir que no estaremos simulando realmente observaciones de VLBI, sino de interferometría conexa, ya que el reloj usado para muestrear las ondas de sonido que llegarán a ambos micrófonos será el mismo.

El primer paso para nuestro experimento es generar un archivo de sonido con ruido blanco, emitido por un solo canal, y prepararlo para su reproducción en un altavoz. Colocamos seguidamente los micrófonos a una cierta distancia del altavoz (un par de metros o más). Es mejor realizar el experimento al aire libre, para evitar reverberaciones, que se traducirían en una correlación residual (por lo que la franja no sería "limpia"). Comenzamos entonces a grabar con ambos micros y reproducimos el ruido blanco.

Tratamiento de la señal

Llegados a este punto, el siguiente paso dependerá de la clase de dispositivo que hayamos usado para la grabación. Si hemos empalmado dos micros a un mismo jack, habremos grabado una señal estéreo, en la que cada canal corresponderá a un micro. Si hemos usado dos micros por separado, habremos grabado dos señales mono, que deberemos unir a un archivo estéreo (un canal para cada micro). Es importante que en este proceso de unión de los canales las señales queden lo mejor sincronizadas posible, para que la franja no salga demasiado descentrada en el espacio de retrasos. Podéis usar programas como IDL, Matlab o Mathematica para manipular vuestros ficheros de audio y programaros vuestro propio correlador en base a los pasos aquí descritos (más abajo encontraréis un script en Python que os permite correlacionar el sonido de los micros en tiempo real). La forma de proceder para calcular las franjas de correlación es la siguiente:

• Aplicar un filtro digital centrado en una frecuencia $\nu_0 =$ 1000Hz con un ancho de banda $\Delta\nu =$ 50Hz (por supuesto, ambos valores pueden alterarse a gusto de cada uno). Este filtro simula el sistema de recepción de las antenas.

• Multiplicar las señales (ya filtradas) por una sinusoide de frecuencia $\nu_0 - \Delta\nu/2$. Este paso simula la multiplicación de la señal por una señal de referencia, proceso conocido como mezcla de cuadratura. En el caso de VLBI, esta señal de referencia la proporciona el máser, el estándar de frecuencia, vía los llamados Osciladores Locales (LO). El resultado es la suma de dos señales, una con una frecuencia centrada en $\Delta\nu/2$ y la otra con frecuencia centrada en $2\nu - \Delta\nu/2$, en virtud de la igualdad:

  
  

  $$\cos{(\nu_0 t)}\sin{((\nu_0 - \Delta\nu/2)t)} = 0.5 \left( \sin{((\Delta\nu/2)t)} + \sin{((2\nu - \Delta\nu/2)t)} \right)$$ (15)

  
  

• Aplicar un filtro digital pasa-baja, de forma que sólo la señal centrada en $\Delta\nu/2$ sobreviva. El resultado es una versión de la señal original, pero corrida en frecuencias desde $\nu_0$ hasta $\Delta\nu/2$. Este paso (similar en todos los receptores heterodinos) es esencial para poder muestrear bien la onda, ya que los sistemas de grabación de VLBI no pueden muestrear ondas con frecuencias tan altas como GHz, pero sí pueden hacerlo a unos pocos MHz.

• Aplicar una digitalización a la amplitud de la señal, de forma que sólo se grabe el signo de la onda (digitalización a 1 bit). Las unidades de grabación actuales en VLBI pueden grabar a 2 o incluso 4 bits, pero por simplicidad usaremos sólo 1 bit. Nótese que en este paso SE PIERDE UN MONTÓN DE INFORMACIÓN SOBRE LA ONDA ORIGINAL, ya que sólo grabamos el signo de la onda en cada momento, no el valor de su amplitud.

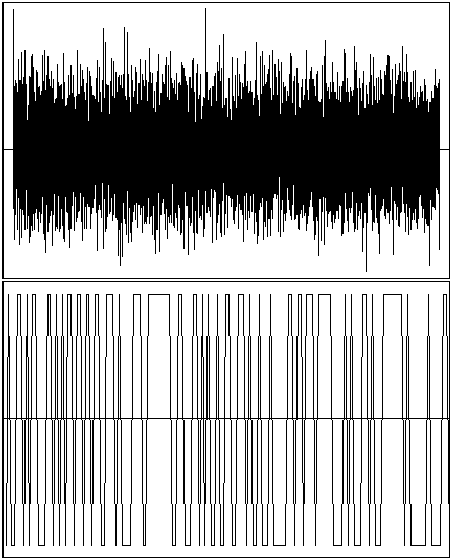
El resultado de aplicar todos estos pasos es una larga serie de 1 y $-1$ para cada micrófono (los signos de la onda en cada tiempo). En la figura 9 se muestra un ejemplo de la diferencia entre la onda original y el vector final formado por el conjunto de 1 y $-1$. Aparentemente, hemos perdido muchísima información de la onda original... Parece increíble que vayamos a poder extraer algo de ese par de vectores llenos de 1 y $-1$, sobre todo teniendo en cuenta que en una observación real de VLBI la contribución del ruido a esa serie de 1 y $-1$ es decenas de veces superior a la de la fuente observada.

Figure 9: Arriba, ejemplo de señal registrada por el micrófono (tiempo en horizontal, amplitud en vertical). Abajo, señal grabada finalmente para la correlación, compuesta por una serie de 1 y -1 (se han unido los los puntos con líneas para mayor claridad visual).

Correlación

Estas series de 1 y $-1$ son entonces grabadas en las cintas (o discos) de cada estación y llevadas posteriormente al correlador. Los siguientes pasos a realizar son:

• Separar los vectores en trozos de 128 elementos. Este número puede cambiarse, pero debe ser igual a una potencia de 2 (a mayor valor, más ancha será la ventana de correlación, es decir, el espacio de retrasos).

• Calcular la transformada rápida de Fourier (FFT) de cada subconjunto de 128 elementos.

• Multiplicar las transformadas de Fourier del micrófono 1 con el complejo-conjugado de las transformadas de Fourier del micrófono 2.

• Calcular las transformadas inversas de Fourier de los productos obtenidos.

El resultado son varias franjas (una por cada subconjunto de 128 elementos) que se podrían representar una al lado de la otra (es decir, representando la matriz delay-time, ver figura 7) o bien se podrían sumar para aumentar la señal respecto al ruido. Este proceso de correlación es conocido como FX (primero transforma en Fourier y después multiplica), en contraste a XF (primero correlaciona y después transforma en Fourier).

En la vida real, la correlación es muchísimo más complicada. Se deben calcular los retrasos entre los radiotelescopios con enorme precisión, para poder tener las franjas suficientemente centradas. Además, se debe corregir el efecto Doppler diferencial, debido a las diferentes velocidades de los radiotelescopios respecto a la fuente, e incluso efectos de Relatividad Especial debidos a dichas velocidades. Normalmente, el correlador referencia todas las señales respecto a un punto que permanece estable (o inercial) durante los pocos segundos que dura la observación de cada visibilidad. Este punto puede ser, por ejemplo, el centro de la Tierra o el baricentro de masas del Sistema Solar. La corrección de la señal de cada radiotelescopio para referirla a estos puntos se hace aplicando rotadores de fase, que no describiremos aquí (básicamente, son operaciones de tipo mezcla de cuadratura, similares a las realizadas por los LO cuando se rebajó la frecuencia natural de la señal para poder ser grabada).

El lector puede modificar el algoritmo aquí descrito y usar osciladores locales con frecuencias ligeramente distintas para cada micrófono durante la mezcla de cuadratura. De esta forma, se introducirá un fringe rate residual en la franja, que podrá apreciarse en la matriz. También puede añadir un retraso entre los canales (es decir, entre las señales de cada micro) antes de la correlación, para ver cómo se traduce esto en un descentrado de la franja en la dirección del retraso. Otra variante del experimento es mover el altavoz, o uno de los micrófonos, durante la toma de datos (por supuesto, de forma suave y constante) para ver el efecto que esto produce en la franja.

Complicando un poco las cosas: mapa de una fuente estéreo

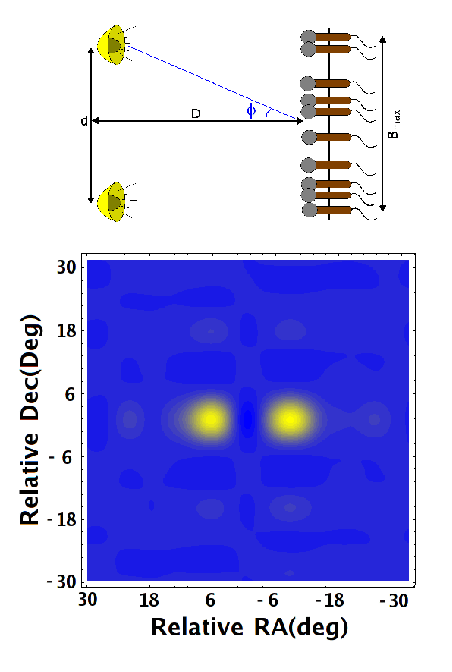
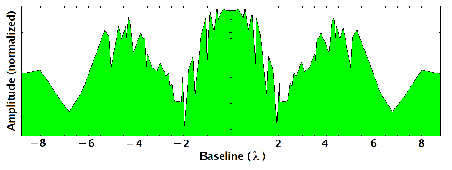
También pueden correlacionarse las señales de más de dos micrófonos, grabando éstas en archivos mono. De esta forma, podemos simular interferómetros más complicados. También podemos usar estos interferómetros para generar imágenes del patrón de sonido observado. Para realizar este experimento, generamos un ruído blanco estéreo y usamos un conjunto de 10 grabadoras digitales. Puede verse un resumen de este experimento aquí. Al correlacionar las visibilidades entre todos los 45 pares de micrófonos, se obtiene una serie de visibilidades en distintos puntos del plano de Fourier. En la figura 11 mostramos las amplitudes de las visibilidades en función de la distancia entre micrófonos (en unidades de la longitud de onda central de observación). Como vemos, la modulación producida por la fuente doble es clara. En la figura 10, también se muestra el mapa acústico de la fuente doble, que se corresponde con las posiciones de los altavoces.

Figure 10: Arriba, esquema de nuestro experimento con 10 micrófonos y una fuente de ruído estéreo. Abajo, mapa acústico obtenido tras la correlación y el cartografiado.

Figure 11: Amplitudes de las franjas de correlación como función de la distancia entre micrófonos (medida en unidades de la longitud de onda central de observación).

En este link encontraréis un script escrito en Python, con en el que podréis generar franjas de correlación en tiempo real, usando dos micrófonos conectados a un mismo jack (tal y como se describe más arriba). Podéis también reciclar el código de este script para programaros el correlador (la parte de la mezcla de cuadratura o la correlación FX). NOTA: en este script no se digitaliza la amplitud a 1 bit antes de la correlación, para acelerar el cálculo en tiempo real y, sobre todo, aumentar la señal a ruido.