|
- Introducción. - Equaciones de Maxwell para el campo complejo |
Es sueño de todo físico que las fuerzas que dictan los fenómenos de la naturaleza sean voces de una misma ley física, una unificación de las interacciones de la materia. Y a mí, como no, el tema siempre me ha atraído, pero, sólo me sé defender algo en el tema de la gravedad elemental y un poco del electromagnetismo básico, de este modo he podido especular mejor con estos campos.
Así pues, a partir de la muy atractiva analogía que existe entre las expresiones de la gravedad de Newton y la ley de Coulomb, he observado una posible solución simple que es común a las dos expresiones.
De este modo, propongo un principio de unificación de estos dos campos a favor del gravitatorio, por simple comodidad. [No obstante, en el último apartado de unificación se toma el otro aspecto del campo Grelma]
Relación carga/masa (volver arriba ↑ )
Observando la ley de Coulomb y la de Newton, podemos pensar que resultan ser la misma expresión si las generalizamos para el campo de valores complejos, de este modo podemos considerar una magnitud como la otra en estado no-real (imaginario) Principio2.
|Feñ = |Fgñ ® – Gm2/d2 ·|urñ = k q2/d2 ·|urñ ® m2 = k/( – G) q2 ® m = k½/( – G)½ q ®
® mq = – (k/G)½ q · i (1)
Hipótesis de la correspondencia carga-masa
La carga no es más que un estado imaginario de la energía, cuya correspondencia con la misma es: E = – (k/G)1/2 · q · c2 · i
El hecho de concebir la carga como una masa imaginaria puede tomar forma inteligible si consideramos el eje de frontera que proporciona la velocidad límite (la luz), es decir, sabiendo que, matemáticamente, una masa que tuviese una rapidez superior a la de la luz se convertiría en masa imaginaria según la relatividad de Einstein (m = mo /a). Esa velocidad sería inaccesible para una fuerza real ya que el espectro másico de una carga real (es decir la masa que le corresponde a una carga) se encontraría en un espacio imaginario (como más tarde se comentará).
Fuerza de campos ( |Fñ ) (volver arriba ↑ )
Si consideramos válida la correspondencia carga-masa, tenemos que decir que toda ley y expresión referida a un campo es válida para el otro aplicando dicha correspondencia, claro está, siguiendo las leyes de la lógica.
F’ñ = –G · Mm/r2 ·|urñ ≡ |F’ñ = k ·Qq/r2· |urñ (2)
|
|F’’21ñ = || |F’ñ || · [ |v2ñ ´ ( |v1ñ ´ |urñ )] /c2 f. magnética |F21ñ = |F’21ñ+ |F’’21ñ f. de campos
|
® |Fñ = –G ·Mm/r2 ·|wñ |wñ = |urñ + [ |v2ñ ´ ( |v1ñ ´ |urñ )] /c2 |
|||||||||||||||||||||||
|
||||||||||||||||||||||||
Culminación de la teoría e implicaciones (volver arriba ↑ )
En el apartado anterior, hemos recordado que la energía asociada al campo gravitatorio era la misma que le corresponde a la fuente, pero de signo cambiado, es decir, la complementaria. Además, sabemos que estas energías son en realidad un exceso de espacio para la masa, y un defecto para su campo gravitatorio., pudiendo así asociar una longitud para la masa (y para su campo). Pero hemos comprobado también que el defecto de energía instalado en el campo gravitatorio se encuentra desde el límite de los acontecimientos (x) hasta el resto del universo (n); no obstante en la primera parte de esta teoría se ha supuesto que dicho defecto de espacio (o energía) se encontraba entre la distancia radial mínima (do) y la máxima; y como hemos comentado en la última parte, parece ser que esto no es así, lo cual repercute en la enunciación del espacio asociado a una masa:
ξ ¹ GM/c2 · ln (n/do)
ξ = GM/c2 · ln (nc2/GM)
Pero este cambio no influye, en lo general, con los resultados obtenidos en la primera parte de este trabajo ya que, aunque nc2/GM no es constante, se puede decir que no varía en general:
ξ = GM/c2 · [ ln (nc2/G) – ln (M) ] en general, M << nc2/G ® ln (nc2/G) – ln (M) ≈ cte
Por tanto, y puesto que lo que importaba era la linealidad entre la masa y su espacio asociado, la corrección no afecta en absoluto a la teoría general de la fenomenología ni a la rededucción de la relatividad restringida (de A. Einstein) que se desprende de ella.
No obstante hay algo muy importante que aparece como consecuencia de esa pequeña corrección, veámoslo:
Si escogemos el caso donde M = nc2/G, entonces es nulo y eso se puede interpretar de la siguiente manera: Dicha masa es tan grande que, al ocupar todo el universo, no puede desplazar el espacio-defecto (campo gravitatorio) a su alrededor y, por eso el exceso que representa esa masa es nulo. Esto significa que la masa del universo es Mu = nc2/G (masa neta del espacio-tiempo de nuestro universo, ya que la masa ordinaria se anula con su campo gravitatorio). Dicha masa se encontraría virtualmente repartida entre los PSETs (puntos de sucesos espacio-temporales), de tal modo que:
d = n/do = s·Mu /mo
siendo d el numero de PSETs del universo
mo = masa en reposo del fotón = ‘s’ veces la masa de un PSET = s·m s
do = distancia radial mínima = radio de un PSET.
De la relación anterior se desprenden las siguientes expresiones:
d = nc2/Gms do = Gms /c2 = Gmo/sc2 n = G Mu /c2
Revisemos también, la energía asociada al campo gravitatorio (h), o complejo: Si Mu es tan grande que no puede desplazar defecto de espacio a su alrededor, sea lo mismo que no tener campo gravitatorio, entonces la energía asociada a él debería ser cero, y por tanto Muc2 sería la energía neta del universo (ya que no se anula con la de su campo). Y efectivamente así es:
h = ∫ [– G Mu2/r2]dr = G Mu2/n – G Mu2/(GMu /c2) = nc4/G – nc4/G = 0
Mu = nc2/G
Por tanto, la energía (y el defecto de espacio asociado) del campo gravitatorio se encuentra distribuida entre GM/c2 y n. ¿Qué hay pues entre do y GM/c2? La respuesta podría ser la siguiente:
Entre do y GM/c2 se encuentra la energía de la masa. De este modo, entre dichas distancias habría el campo positivo (masa) en oposición al campo negativo (gravedad), y también tendría una energía asociada (h’), que sería, por supuesto, Mc2. Pero, claro, esto significa que cabría definir una autofuerza especial para dicho intervalo, que indicaría como se distribuye la energía positiva. Así pues propongo la siguiente expresión para h’ (siendo su campo de predominio do y GM/c2, pero, como en un fotón, realmente el campo energético-positivo se extiende por todo el universo):
h’ = ∫ [Mc2do/r2]dr = ∫ [GMms/r2]dr = Mc2 – msc2 Intervalo principal (do, GM/c2) [do = Gms/c2]
h’ = ∫ [Mc2do/r2]dr = ∫ [GMms/r2]dr = Mc2 Integral para todo el dominio de h’(do, n)
[y’] = GMms/r2 Puesto que está definido como una autofuerza, (Mms)½ = M’
[y’] = GM’2/r2 ® g = [y’] / M’ = G(Mms)½ /r2 ® V = G(Mms)½ /r
De este modo, el campo gravitatorio (el potencial) sería discontinuo en el punto GM/c2, y estaría definido de la siguiente forma [para toda masa, real o compleja]:
|
V = |
= G(Mms)½ /r |
r Î [do , GM/c2] |
| = GM½ /r · [ms½ – M½] ≈ – GM/r2 | r Î ]GM/c2, n] |
Adviértase, entonces, que con esta corrección de la teoría neo-clásica, tenemos resultados distintos para la cronomecánica en las cercanías de un agujero negro, pues, por ejemplo ya no se podrá viajar al pasado, ni desaparecer de la realidad espaciotemporal estándar. Por otro lado eso supone un alivio para la integridad de los sucesos.
Ilustración 7
Matización de la ilustración 6. Representación de las lineas de espacio en respuesta al potencial gravitatorio (V).
r = GM/c2 mientras que x = distancia entre el potencial mínimo y el pto. de inflexión. Parece ser que en la realidad x = 0, es decir los dos ptos. coinciden.
Tengamos en mano les expresiones de las autofuerzas primaria y secundaria:
[y’] = GMms/r2 r Î [do , n] autofuerza primaria
[y] = – GM2/r2 r Î [GM/c2, n] autofuerza secundaria
Otra cosa que cabe revisar es la definición de ‘límite de los acontecimientos’ pues ha de ser una distancia real, y tal como hemos definido (para toda masa compleja) se convierte en un número complejo. De este modo pues:
x = G||M||/c2
De este modo tenemos una expresión general para las energías asociadas al campo complejo. [Integral definida ={inf , sup}∫ ]
h’ = {do, n}∫ [GMms/r2]dr = Mc2 "masa compleja [do = Gms/c2]
h = {GM/c2, n}∫ [GM2/r2]dr = – ( M2 / ||M|| )c2 "masa compleja
La energía asociada a la autofuerza primaria se correspondería igualmente con la energía de la fuente. Ahora bien, la integración de la autofuerza secundaria es distinta a la inicial, siendo en este caso, como resultante una energía real aunque la masa sea compleja. Así pues, en el caso de la gravitación ordinaria, resulta ser la energía opuesta a la fuente (manteniéndose las leyes de la conservación del espacio efectivo total y real), pero en el caso de la electroestática (y por tanto, del electromagnetismo) la energía asociada a los campos es siempre positiva, lo cual indicaría que, para formar un diferencial de potencial eléctrico a partir de un sistema en conjunto neutro, se precisa de la aportación de energía (que será empleada para ‘constituir’ los campos). Y esto está de acuerdo con las leyes del electromagnetismo; miremos, por ejemplo, la energía (positiva) asociada al campo de una onda electromagnética.
Por el contrario, para formar campos gravitatorios no se precisa de energía en un balance neto, ya que las energías se compensan. Por esta razón, podemos tener una idea de lo q entraña la energía: nada, ya que toda ésta se verá “anulada” (en sentido de balance) por su campo gravitatorio. Y de aquí surge la paradoja: “la conservación de energía sugiere que la energía se creó”. Esto es: según parece, podríamos formar masas (energías positivas) junto con sus campos gravitatorios, ya que el balance energético sería el mismo (conservación).
La solución a esta paradoja está en recordar como se entendió el sistema gravitatorio, que era como la transmisión de un pulso del espaciotiempo. Observemos pues que ocurre en el aire cuando le damos una nota (“impulso”): se crea una zona de presión positiva y otra de presión negativa respecto al estado calmado (en analogía presión-energía) pero gracias al impulso que nosotros le hemos dado al aire. Esto es, habíamos creado una zona de presión positiva (analogía con la “creación” de masa) gracias a que hemos introducido un impulso, la nota (analogía a la masa que se adentra en un sistema de espaciotiempo abierto). Por tanto, para “formar” masa se necesita la introducción de ésta (al menos en forma de energía).
Una vez comprendida las correspondencias enegéticas y espaciales de las cargas (es decir, de sus campos de autofuerza), observemos la definición, para las cargas, de las parejas de espacio-imaginario/espacio-real que se desprende del principio de equivalencia entre masa (en este caso imaginaria) y espacio. Pues, tendríamos, para cada carga, un espacio imaginario (campo de autofuerza primaria) y otro real (campo de autofuerza secundaria), con ξ = GM/c2 · ln (nc2/GM).
De este modo, pese que no existe anulación (o compensación) energética (o espacial) entre los dos campos de autofuerza de una misma carga (cosa que si que ocurría para la masa), la conservación del espacio efectivo total se cumple conjuntamente para el sistema dual de cargas: Entre un espacio no perturbado y el mismo espacio una vez formado un sistema dual de cargas, se conserva la carga (energía imaginaria), la energía real asociada a los campos y (por tanto) el espacio efectivo total. En cambio, si una carga individual se adentra en un zona de espacio imperturbado, se viola, aparentemente el principio anterior; pero, si observamos de más de cerca la carga que se manifiesta en dicho espacio, observaríamos que se rodea de cargas virtuales opuestas, como intención de cumplir el principio. Se trata pues de la polarización del vacío (vestimenta de una carga), que se correspondería con un campo secundario (muy débil) asociado al campo de la autofuerza primaria de una carga.
Por último, para completar el análisis de la unificación gravitoelectromagnética (grelma), debemos prestar atención al caso del magnetismo asociado a la gravedad no estática. Observaremos, pues, un caso concreto de magnetismo gravitatorio al que llegaremos del caso general de la fuerza de Lorentz. La intención de este estudio será proponer un experimento que intente demostrar la validez de la teoría.
Fuerza de Lorentz: |urñ = |rñ/||r|| |u1ñ = |v1ñ/||v1|| |u1ñ = |v1ñ/||v1||
m =hn/c2
|F21ñ = – GMm/r2 · { |urñ + [ |v2ñ ´ ( |v1ñ ´ |urñ )] /c2}
1-Caso de dos fotones cualesquiera: ||v1|| = ||v2|| = c
|F21ñ = Gh2n1n2/c4r2 · { [ |u2ñ ´ ( |u1ñ ´ |urñ )] – |urñ }
2-Caso de dos fotones de direcc. paralelas: Sentidos: u1 = ±1 u2 = ±1
|F21ñ = Gh2n1n2/c4r2 · (u2u1 –1) · |urñ
3-Caso de dos fotones iguales, de la misma dirección y sentidos contarios:
|F21ñ = 2Gh2n2/c4r2 · |urñ = 2·|Fgravit.ñ
|a totalñ = 2·|Fgravit.ñ / m = 2·|gñ
4-Caso de dos lásers iguales, de la misma dirección y sentidos contarios:
Ien. = intensidad de energía = de/dt
J = factor de correspondencia = (G/k)1/2 ·i
El láser 1 provocará una intensidad gravitatoria (g) en el punto P situado en el haz del láser 2. Dicha intensidad resultará de la suma entre las intensidades dg que provocan las secciones dm del láser1. R << L
Disponemos de dos lásers idénticos pero de intensidad energética (Ien) con sentidos opuestos. A cada láser podemos asociar una masa M = Ien t /c2 = Ien L/c3 , y también una densidad lineal másica: l = dm/dl = M/L = Ien /c3.
dg = – Gdm/r2 = - G ldl/r2 r2 = R2 + l2
dg = – G ldl / (R2 + l2) 1/(R2 + l2) = 1/R · [1/(1 + (l/R)2) · (1/R)]
g = {a,b}∫ – G l / (R2 + l2) · dl = – [Gl/R · atg(l/R)]
|
P está en la posición x: a b g 0 -L/2 L/2 – Gpl/R cercana a 0 -L/2 L/2 – Gpl/R -L/2 0 L – Gpl/2R L/2 -L 0 – Gpl/2R
|
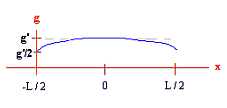 |
Si L >> R, la intensidad gravitatoria (g) a lo largo de las posiciones (x) se mantiene más o menos constante con un valor g’ = – Gpl/R.
Como hemos deducido en el caso 3, la aceleración total (|a totalñ) que sufren los fotones de sentidos opuestos (una aceleración que es normal a la trayectoria) es igual al doble de la intensidad gravitatoria de la trayectoria de los fotones. Así pues:
|a totalñ = – 2pGl/R · |u Rñ t = L / c
La desviación = DR = || a total || t2/ 2 DR = pGlL2/Rc2 = pG Ien L2 / Rc5
El experimento debería realizarse en un lugar del espacio donde g << g’ y también se debería intentar que L >>> R, así como tener una Ien muy muy alta.
Con todos los datos del caso
anterior, podemos idear un experimento, prediciendo la desviación (DR),
para así hacernos una idea sobre la precisión que se requiere para demostrar la
validez de esta teoría.
En primer lugar, averigüemos que valores deberían tomar L, R y Ien para poder realizar una medición fiable. Pensaremos el experimento para tres lugares:
1 – La Tierra: desierto de Sáhara. Dos torres separadas por 1200 km: Atlas-Ahaggar
desierto de Austalia. Separación 1100 km: Mt_Newman-Sas. Musgrave.
La aceleración de la gravedad no repercutiraá en la desviación descrita anteriormente ya que esta es horizontal y la de la gravedad es vertical (y para los dos lásers).
Pongamos una separación de los lásers de 1 mm. ¿Qué intensidad han de tener los lásers para q se observe una desviación de 1mm?
DR = pG Ien L2 / Rc5 Unidades del S. I.
10 – 6 = p · 6’67 · 10 – 11 Ien (1’2·10 6)2 / (10 – 3 · 2’99795·1040) Ien = 8’025 · 1030 J/s
2 – Satélites artificiales: Dos satélites estacionarios entre sí, separados por 100.000km, con radio a la Tierra de 50.000 km.
Se debería conseguir una estaticidad relativa perfecta entre los dos satélites durante unos segundos, algo casi imposible.
Hagamos la misma pregunta.
10 – 6 = p · 6’67 · 10 – 11 Ien · (10 8)2 / (10 – 3 · 2’99795·1040) Ien = 1’156 · 1027 J/s
3 – Luna-Plutón: Nuestra Luna y un planeta exterior, Plutón. Distancia aproximada 6 · 1012 m.
Debido a la “estaticidad” de la Luna y el gran período sideral de Neptuno, hace que, dicho sistema, sea un “buen” candidato para el experimento.
Aquí tenemos el problema del tiempo: la duración requerida para el experimento (debido a la finidad de la luz), así como el tiempo de espera para preparar el experimento.
Hagamos la misma pregunta.
10 – 6 = p · 6’67 · 10 – 11 Ien · (6·1012)2 / (10 – 3 · 2’99795·1040) Ien = 3’21 · 1017 J/s
La cuestión es: ¿nuestra tecnología permite que algunos de estos candidatos sea viable para el experimento ideado? ¿o tendremos que jugar con espejos para no tener que extender el experimento a una escala inaccesible? De igual modo, si queremos imitar la distancia de la Luna a Plutón encerrando el recorrido de los lásers entre espejos, necesitaríamos una cantidad bestial de ellos y de condiciones perfectas, las cual cosa sería igual o más difícil que hacer viable tercer candidato.
El tiempo dará la respuesta.
Cuantificaciones de las magnitudes (relacionadas con el campo complejo): (volver arriba ↑ )
- distancia = k·do kmax = n/do = d
- masa = j·mo lmax = s·Mu /mo = d s = 1 ó 3 exclusivos
jmov /a = p = h/kdo ® a = kjdomoc/h ® a = kjGmo2v /shc2 "partícula
| Para el fotón: j = 1 v ≈ c ® | a = kGmo2/shc |
La energía total (Et) para el fotón es:
Et = moc2/a = shc3/kGmo a = 1 ® k es máximo: kmax = shc/Gmo2 = d
Ídem: a·moc2/a = b·moc2 a = b/a ® amin = 1/d, si k =1 ® d = 1/a = shc/Gmo2
| Mu = d mo/s = hc/Gmo = nc2/G |
Et = shc3/kGmo = hn n = sc3/kGmo t = 1/ n = kGmo/sc3
|
to = Gmo/sc3 |
Tenemos pues una cuantificación para el tiempo:
- tiempo = k· to to = Gmo/sc3 = do/c
Cumpliéndose que: Muc2 · to = h
Además podemos calcular el límite inferior de la masa en reposo del fotón (mo), y con ella, los límites de otras magnitudes. [Primera aproximación]:
Sea T la edad del universo (≤ 6’12 ·1017 s.), R su radio real, n el radio aparente.
n ≈ pR (en un principio) R ≤ T·c ® n ≤ T·c·p = 5,65 · 1026 m.
mo = h/cn ≥ 3’90 · 10 – 69 kg. no cte ms = mo/s ≥ 1’30 · 10 – 69 kg. no cte
do = Gms /c2 ≥ 9’7 · 10 – 97 m. cte d = n/do ≤ 5’8 ·10 122 no cte
Mu = hc/Gmo ≤ 7’6 · 10 53 kg cte to = do/c ≥ 3’2 · 10 – 105 s. cte
También deberíamos tener que:
moc2 ·T = h ® mo = h/ Tc2 = 1’2 ·10 – 68 kg
Con lo cual deducimos que la velocidad (V) de expansión radial del universo puede ser:
V ≈ c/p
Se dice que la densidad (l) de la energía del vacío es constante, pero yo creo q lo que es constante es la masa del universo (Mu):
l = Mu /n = ms/do = c2/G ¹ cte.
(volver arriba ↑ )
© 2004 ROBERTO MONCHO
_____________________________________________________________________________________________________
A- Espacio-tiempo en el campo gravitatorio (Relatividad General)
B- Fuerza Gravitoelectromagnética (Grelma).
D- Interacción Fuerte-Débil-Grelma (FDG)
|
© 2004 ROBERTO MONCHO |