A- Espacio-tiempo en el campo gravitatorio (Relatividad General)
|
A- Espacio-tiempo en el campo gravitatorio (Relatividad General) |
El honorable genio Albert Einstein fomentó una teoría general sobre la curvatura de espaciotiempo, pero… a qué se debe esta curvatura? ¿Qué leyes dictan que una masa (o energía) curve el espacio? Desde mi constancia de la existencia de la teoría de Einstein me he preguntado el porqué, y supongo que como otros muchos más. Intentado responder a esta pregunta he teorizado sobre una posible correspondencia directa entre energía y espacio, y sobre sus consecuencias directas e indirectas sobre el marco general de la física.
Es este documento, pues, una propuesta de base teórica para unificar conceptos y leyes de la física.
Constancia absoluta de la
energía total de un sistema perturbado de espacio.
(volver arriba
↑ )
Hipótesis de la curvatura-compensación
La curvatura espacial (o defecto de espacio) existe como una compensación al exceso de espacio que representa una masa.
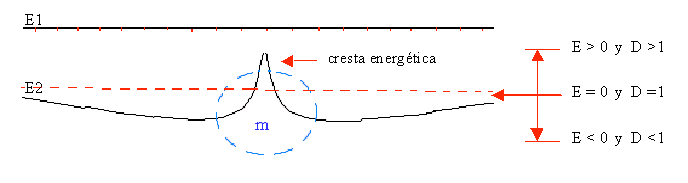
Una masa M crea una curvatura espaciotemporal (o campo gravitatorio) tal que efectúa un estiramiento del mismo espaciotiempo para compensar el defecto de espacio* generado por la presencia de la vibración* (o energía) total de la masa, magnitud que representa una concentración de espacio. Es decir, cabe entender a la masa como una estado vibratorio del espaciotiempo, análogamente a la vibración de una cuerda de goma, cuya cresta representaría la masa, y las dos depresiones corresponderían al campo gravitatorio, con la única diferencia que, en el caso de la masa, la cresta se encontraría inmensamente plegada sobre sí (por la "complejidad" de las aparentes cuatro dimensiones, y sobre todo porque la masa es un estado energético entramado por las cargas eléctricas). La masa se mueve como lo hacen las vibraciones. La masa es como un anticiclón encerrado en una "esfera" y rodeado por una depresión atmosférica (campo gravitatorio) que se suaviza con la distancia.
*Definiciones:
espacio: puesto que espacio y tiempo se unen en un mismo concepto, espacio pasará a ser un sinónimo (parcial) de tiempo y de espaciotiempo, como la energía lo es de la masa (energía-carga) y de la carga [ver teoría de la fuerza electrogravitomagnética].
vibración: una vibración
suma de todas sus partículas elementales (fotones reales, y no fotones
imaginarios (o de carga) porque estas ondas se anulan entre sí) [ver teoría
de la fuerza electrogravitomagnética].
|
Ilustración1 |
||||||||||
 |
||||||||||
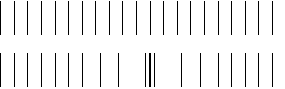 |
En el caso de una onda longitudinal la cresta corresponde a la zona donde mayor densidad de "líneas" hay, disminuyendo ésta en las inmediaciones. Esto ilustra el concepto de la densidad de espacio. Pero los dos tipos de onda son la misma cosa, pero vista desde perspectivas diferente (una es de 2 dimensiones y la otra de tres, pero matemáticamente es lo mismo) |
|||||||||
|
Sea el espacio-tiempo como una goma elástica donde la energía (masa) es vibración de la misma. Obsérvase que el espacio inicial (E1) se ve perturbado por la masa (m) que representa la cresta de una onda (cambiemos el tipo transversal por longitudinal conceptualmente), donde la densidad de espacio (D) es mayor que 1, en detrimento de las zonas cercanas, donde la densidad decae a menos de 1. Más adelante observaremos que las densidades pueden corresponderse a distintos estadios de energía
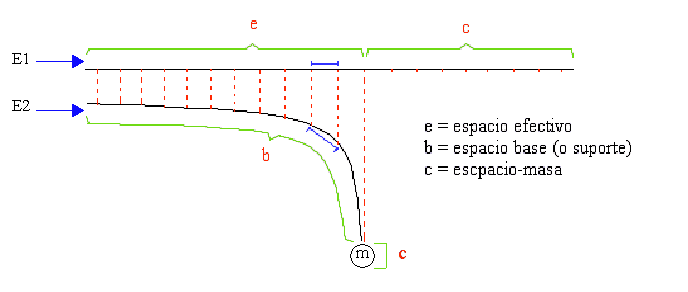
Para mejorar la comprensión de la curvatura espacial, nosotros la estudiaremos como si el espacio tuviese una única dimensión (curiosamente, más tarde veremos que matemáticamente es posible, e incluso recomendable, reducir el espectro de las cuatro dimensiones a una, que llamaremos distancia radial -o tiempo-). De este modo cabe insertar nuevos conceptos: Espacio efectivo (e): Espacio distancial que habría en una región si ésta no estuviese perturbada por una masa (es decir, el espacio que todavía no se ha estirado o dilatado). Es el espacio que recorre la luz, es decir el espacio que observamos aunque esté deformado intrínsecamente por un campo gravitatorio (ya que la luz recorre la misma distancia en un mismo tiempo esté o no deformado el espacio). Lo llamaremos también espacio lumínico, espacio observado, espacio real y espacio inicial, (puesto que lo consideramos un espacio anterior a su perturbación). Espacio base (b): Espacio distancial "ocupado" por el espacio efectivo, que ha podido ser estirado o no (si ha sido estirado, b será mayor que e, sino, serán iguales). Es el espacio que recorre un cuerpo en caída libre, si su velocidad es mucho menor que la de la luz, por eso lo llamaremos también espacio del viajero (frente al espacio observado); así como espacio suporte, espacio físico (frente a real) y espacio final (frente a inicial). Efectividad o densidad de espacio (D): Razón (cociente) entre el espacio efectivo y el espacio base. Es la relación entre el espacio de interacción (el lumínico o real) y el espacio del viajero (el físico). D = e / b Sea una región, con un espacio inicial no perturbado, todo ese espacio es efectivo y coincide con el espacio base. Dicho espacio total no puede variar, es decir: En un sistema abierto (o cerrado) de espacio base-efectivo, la suma de los espacios efectivos (estén en el estado en que estén) será constante y será igual al espacio base. (Principio de constancia del espacio efectivo total Principi1). Consideremos una región del universo casi no perturbada por ninguna masa (esto es, D = 1, aprox.). Cabe apuntar, primero, que "abierto" hace referencia a "abierto respecto al resto del universo físico" (no exterior a él). De repente una masa se adentra en el sistema. ¿Qué ocurre?. La masa representa una vibración del espacio, es decir, no incorpora espacio nuevo (de la misma manera que una onda ordinaria no traslada materia), de este modo, el espacio inicial sólo tiene que estirarse para compensar al "exceso en densidad" que la masa representa (ver ilustración 1). Pero, entre el paso de la situación 1 a la situación 2 a sucedido algo especial. Puesto que el espacio efectivo total debe mantenerse constante y la masa representa un tipo de espacio efectivo concentrado, este espacio debe ser restado de sus inmediaciones, de tal manera que el espacio efectivo accesible disminuye (pero no el total). Esto es, parte del espacio efectivo inicial se emplea en "vibrar" el cuerpo incorporado al sistema, a ese espacio lo nombraremos espacio masa (c), y al nuevo espacio efectivo resultante (el accesible), lo llamaremos simplemente espacio efectivo (no confundir con el espacio efectivo total del sistema). El espacio base de un sistema siempre es constante puesto que representa la constancia espacial de dicho sistema abierto, pues es la referencia (el estado inicial del espacio efectivo accesible). |
||||||||||
| Ilustración2 | ||||||||||
 |
||||||||||
|
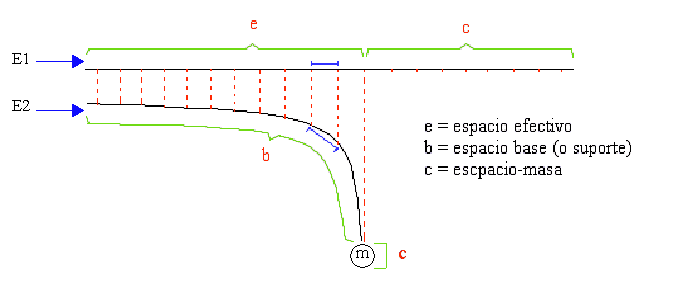
Puede observarse como el espacio inicial (E1) queda defromado por la presencia de la masa (m), que representa el espacio c ("concentrado"). Pero el espacio base (b) sigue seiendo el mismo que E2, sólo que el espacio efectivo se ha reducido (hasta e) al ser usado parte de él en la construcción de la masa (c), de este modo, b sólo está ocupado por e, disminuyendo la densidad del espacio E2 al rededor de m. se considera espacio base al equivalente de espacio (efectivo) que no está deformado por una masa (es decri, que se halla lejos de ella).
La primera consecuencia teórica es la relatividad general de la fenomenología: un cuerpo en caída libre tendrá una inercia propia virtual (principio de inercia del viajero *) que, según el observador no posee, sino que el cuerpo sufre una aceleración. Esto se ve bien en el efecto doppler en un campo gravitatorio: una luz monocromática de frecuencia n tiene una dirección de caída libre; la propia luz cree que su n es constante, pero un observador ve que la n va aumentando a medida que decrece la distancia a la masa gravitatoria; esto es así porque la luz viaja por el espacio físico (el base como todos lo cuerpos, aunque recorra un espacio efectivo), de este modo, la constancia propia de la frecuencia frente al aumento de la dilatación del espacio efectivo, se traduce para un observador (que sólo ve el espacio efectivo) en un incremento de la frecuencia (ver ilustración 3).
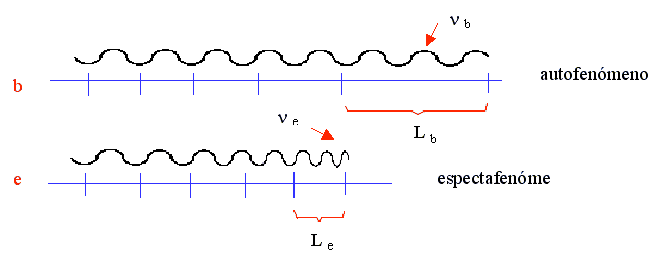
Relatividad General de la Fenomenología (volver arriba ↑ ) Estudiemos el efecto Doppler gravitacional desde más cerca: Consideremos dos perspectivas, dos marcos fenomenológicos distintos, uno para el objeto en estudio (el viajante) y el otro para el observador. Al fenómeno tenido lugar en el primer marco lo llamaremos autofenómeno y al visto por el observador, lo denominaremos espectafenómeno. En el autofenómeno, la frecuencia de la luz permanece constante mientras el espacio se va dilatando a sus pies (el espacio efectivo accesible se está estirando y ya ocupa el espacio b), por contra, en el espectafenómeno (el fenómeno própiamente dicho) el que permanece constante es la unidad de longitud L e , en detrimento de l e (ya que ne aumenta).
|
||||||||||
| Ilustración3 | ||||||||||
 |
||||||||||
|
Obsérvase como L b crece análogamente a ne , mientras que L e y nb permanecen constantes. Esta dualidad representa un mismo fenómeno pero visto desde dos perspectivas distintas, se trata pues de un ejemplo de relatividad de espacio curvado. La constancia de nb responde al principio de inercia propia *, mientras que la constancia de L e (unidad de espacio efectivo) permanece constante ya que la velocidad de la luz lo es y el espacio efectivo es el observado. |
||||||||||
| Principio (o hipótesis) de inercia propia:
Un cuerpo que tiene una frecuencia n en una región del espacio de D = 1, la mantendrá, según su propia perspectiva, pese a adentrase en zonas de D ¹ 1, así como también lo harán todas las magnitudes directamente relacionadas con la frecuencia (a, t, etc.), de tal modo que experimentarán variaciones para un observador en respuesta a la variación de D.
|
||||||||||
|
Según mi intuición, pues, L e = cte. ne ® aumenta nb = cte. L b ® aumenta |
® ne / L b = cte ® |
ne / L b = nb / L e |
||||||||
|
ne / L b = nb / L e ® |
ne / nb = L b / L e ® |
lb / le = L b / L e Para la long. de onda estacionaria (l)
|
||||||||
|
La relación ne / nb es fácil de sacar, sólo hay que aplicar que DEm = 0 (conservación de la energía mecánica relativista) y que nb equivale a la ne que tendría el cuerpo si estuviese muy lejos de la masa (recordemos que ne = f(r), puesto que aumenta al disminuir r -distancia a la masa-). Consideremos dos nb distintas: n1 y n2. Aplicando DEm = 0, con: DEc = moc2(1/a2 -1/a1), m = mo /a a = (1 – v2/ c2)1/2 DEp = -GMmo (1/a2r2 – 1/a1r1) Y para la luz: DEc = h(n2 - n1), m = hn/c2 DEp = (-GMh/c2 )·(n2/r2 - n1/r1)
|
||||||||||
|
n2
/
n1=
[r2 (r1 c2 - GM)] / [r1 (r2
c2 - GM)]
3
Efecto Doppler gravitacional |
VER AP.
5 |
|
||||||||
|
l2
/
l1=
[r1 (r2 c2 - GM)] / [r2 (r1
c2 - GM)]
4
Longitud de onda estacionaria |
VER AP.
7 |
|||||||||
|
a2
/
a1=
[r1 (r2 c2 - GM)] / [r2 (r1
c2 - GM)]
5
Cantidad de reposo |
VER AP.
6 |
|||||||||
| Ahora encontramos la relación de ne / nb, sabiendo que es la misma que n2 / n1, si n1 es la frecuencia del cuerpo de caída libre situado lejos de la masa central, es decir: | ||||||||||
|
ne / nb = lim ( n2 / n1 ) r1 ® ∞
|
3® ne / nb = lim{[r2 (r1 c2 - GM)] / [r1 (r2 c2 - GM)] ® r1 ® ∞ |
|||||||||
|
®
ne
/
nb
= (r2c2) /(r2 c2 - GM)
® ® L e / L b = 1 – GM/r2c2 1®
|
nb / ne =(r2 c2 - GM) / (r2c2) ® D = 1 + V/ c2 6 |
nb
/
ne
= 1 – GM/r2c2
® DENSIDAD DE ESPACIO Espacio efectivo sobre espacio soporte |
||||||||
|
Otra implicación teórica es la contracción de la longitud de un viajante visto por un observador ajeno. Si bien esto puede deducirse directamente por la expresión 5, que ha salido directamente de la física actual, es bueno deducirlo desde la nueva teoría para así aportar argumentos a su favor; de este modo usaremos también la expresión 2 y la 7, que son de esta teoría: |
||||||||||
|
L e / L b = D = 1 + V/ c2 (7) lb / le = L b / L e (2) |
" le / lb = 1 + V/ c2 " Para el fotón y por tanto para las longitudes en general |
l e / l b = 1 + V/ c2 8 |
||||||||
|
Siendo l e la longitud impropia y la l b la propia, ya que l e es la que el observador ve.
|
||||||||||
|
Y según la relatividad especial (y aplicando la expresión 5): a2 / a1= [r1 (r2 c2 – GM)] / [r2 (r1 c2 – GM)] (5) |
||||||||||
|
l i1 = a1 · l p l i2 = a2 · l p
|
® l i2 / l i1 = a2 / a1 ® |
l i2 / l i1 = [r1 (r2 c2 – GM)] / [r2 (r1 c2 – GM)] | ||||||||
|
l e / l b = l i / l p = lim (l i2 / l i1) r1® ∞ |
® l e / l b = (r2 c2 – GM) / (r2c2) ® l e / l b = 1 – GM/r2c2 | |||||||||
|
l e / l b = l i / l p = 1 + V/ c2 (8)
|
||||||||||
|
Y del
mismo modo (tanto de una forma como de otra) puede deducirse la dilatación
del tiempo en el campo gravitatorio:
Desde el punto de vista de esta teoría, el tiempo es simplemente la inversa conceptual del espacio (VER AP 9): El producto de espaciotiempo l·t es constante (para todas las posiciones en el campo gravitatorio), de tal modo que si el uno se dilata, el otro se contrae. Es como una superficie virtual del universo que es constante para un instante determinado. Si l·t = cte. es porque l y t son la misma cosa, pero vistas desde dos perspectivas distintas (es como el autofenómeno y el espactafenómeno: mientas la longitud de espacio se dilata en el autofenómeno la longitud del viajante se contrae en el espactafenómeno, lo que en uno aumenta en el otro tiene que disminuir, como el principio de causa-efecto; así pues, si el espacio del viajero se contrae en la gravedad, su tiempo ha de dilatarse (o, lo que es lo mismo, su velocidad del tiempo ha de disminuir). De este modo podemos aplicar l·t = cte, para deducir cómo se dilata el tiempo (es decir, como se contrae su velocidad). Sea l b = longitud propia del viajante. Sea l e = longitud impropia del viajante (la observada). Sea t b = tiempo propio del viajante. Sea t e = tiempo impropio del viajante (el observado). l e · t e = cte. (antes de acercarse a la masa gravitatoria, l e = l b y t e = t b, por tanto:) |
||||||||||
|
l e · t e = l b · t b ® l e / l b = t b / t e |
8® t b / t e = 1 + V/ c2 ® t p / t i = 1 + V/ c2 | |||||||||
|
y definiendo t (velocidad del tiempo del viajero respecto el observador) como t = t p / t i (t es como una frecuencia: "al viajero le pasan tantos segundos de vida por cada segundo de los nuestros"). |
t = 1 + V/ c2 9 |
|
||||||||
|
Como decía, este mismo resultado puede obtenerse directamente por aplicación de la relatividad de Einstein: |
||||||||||
|
l e / l b = l i / l p = 1 + V/ c2 (8) l i / l p = a (sabemos) |
® a = 1 + V/ c2 (10) |
[a = (1 – v2/ c2)1/2] | ||||||||
|
t p = t i · a ® t p / t i = a a = 1 + V/ c2 (10) |
® t = 1 + V/ c2 (9) |
|||||||||
|
Observemos que esta a está expresada de tal forma que suponemos un sistema ideal de referencia: caída libre desde el “reposo”, respecto la masa central. Es decir, se trata de una simplificación de todo el entramado de relatividad, definiendo unas situaciones iniciales como referencia: posición muy lejana a la masa central, donde suponemos el tiempo con transcurso natural, longitudes propias y masa en reposo (propia) del viajero. También podemos observar que, como los efectos producidos sobre la luz reflejan la situación fenomenológica del espacio-tiempo, tenemos que la frecuencia de la luz (n) informa sobre la frecuencia del tiempo (t), pues son consecuencias del tipo causa-efecto que responden a la relatividad general de la fenomenología: |
||||||||||
|
ni/np = tp/ti ni = np /D tp = 1 |
® ti = tp ·D ® t = D (9) |
|||||||||
|
De esta manera encontramos
que la frecuencia del tiempo respondería también a la dualidad autofenomeno-espectafenómeno
en correlación con la frecuencia ondular del viajante. Las implicaciones teóricas de todo esto son inmediatas: desde teorizar sobre viajes al pasado hasta especular sobre la relación directa entre espacio y masa (o energía). En primer lugar, cabe proponer una correspondencia de espacio-energía, para lo cual supondremos que la curvatura intrínseca del espacio que representa una masa es independiente de su forma, aunque observemos una manifestación diferente debido a que la masa (el espacio que representa [“positivo”]) está ocupando un espacio extra (“negativo”) que neutraliza ligeramente la curvatura total dentro de la masa (por ejemplo: un planeta). Así pues le asignaremos un espacio (en un principio, unidimensional) a una masa M, que corresponderá al defecto de espacio que hay en sus alrededores. Recordemos que nosotros observamos un espacio eficiente e que “ocupa” un espacio mayor b, al que llamábamos espacio base, y puesto que “sabemos” la relación entre e y b por medio de la expresión de densidad de espacio D (expresión 7). Además, concluimos anteriormente que el espacio inicial (o espacio base b) es igual a la suma del espacio efectivo final de los alrededores (e) y el espacio correspondiente a la masa (c), es decir: b = e + c. También cabe poner unos límites al espacio (de los que hablaremos más adelante en la parte dedicada al universo), estos son ‘n’ (radio aparente del universo) y ‘do’ (distancia radial mínima entre dos sucesos).
|
||||||||||
 |
||||||||||
|
Así pues podemos deducir lo siguiente: Puesto que la densidad D viene en función de cada punto del espacio efectivo (D = 1 + V/ c2, donde V es el potencial gravitatorio), entenderemos que la forma general D = e / b no es de gran ayuda para determinar el espacio total b, por eso cabe aplicar diferenciales (d). De este modo, D = de/db. Sea e el espacio de referencia total que envuelve a una masa, desde su centro (do) hasta la distancia lineal (o radial) máxima del universo (n).
|
||||||||||
|
D
= de/db ®
db = D · de ® ∫e
db =
∫b
D·de ® b
= ∫e
(1 + V/ c2)·de ® ® b = {sup = n}∫do (1 + GM/rc2)·dr ® b = (n - do) + GM/c2 · ln (n/do) ® b = e + GM/c2 · ln (n/do) Y a partir de la definición: b = e + c ® c = b – e ® c = GM/c2 · ln (n/do) (11)
|
||||||||||
|
ξ = GM/c2 · ln (n/do) |
11 |
NOTA: Esta expresión es una primera aproximación de lo que será la relación entre masa y espacio, que perfeccionaremos en el próximo capítulo. | ||||||||
|
Para distinguir el espacio-masa (c) de la velocidad de la luz (c) hemos cambiado la notación del espacio-masa por la letra griega ξ |
||||||||||
|
Esa es, pues, la expresión que propongo para cualquier masa (o energía E = mc2), siendo incluso más general (para todo campo conservatorio), como más adelante expondré. Además, a partir de la expresión de la densidad de espacio (o densidad espacial del espacio), el mismo espacio puede tomar forma si simplificamos su curvatura a una línea (la dimensión radial). |
||||||||||
| Ilustración4 | ||||||||||
 |
||||||||||
|
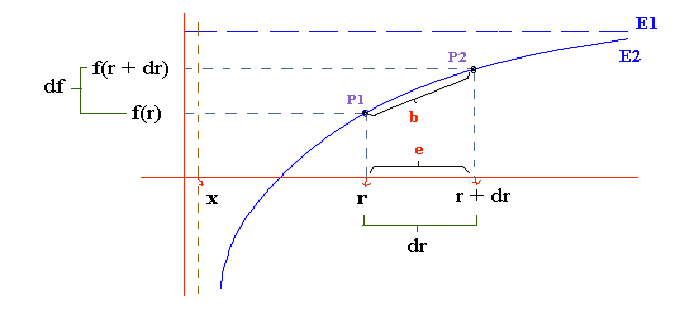
Imagínese que el espacio efectivo (e) [que es el de nuestra referencia observacional] correspondiente al espacio físico (b) es la proyección del espacio (b) sobre un eje de las abcisas (de distancias absolutas y radiales [r] ). La curva entre dos puntos cualesquiera del espacio física, es decir P1 y P2, tiene un valor longitudinal mayor o igual que el efectivo (distancia entre sus proyecciones).
|
||||||||||
|
Sea e/b = D, Encontremos pues la función de la curva del espacio [f(r)]. |
||||||||||
|
e = dr b = |P2 – P1| P1 = (r, f(r)) P2 = (r + dr, f(r + dr)) |
® P2 – P1 = (dr, f(r + dr) – f(r)) = (dr, df) | |||||||||
|
b = |(dr, df)| = [dr 2 + df 2]1/2 |
||||||||||
| dr 2 + df 2 = b 2 = (e/D) 2 ® dr 2 + df 2 = (dr · 1/D) 2 ® (dr 2 + df 2 )/ dr 2 = (1/D) 2 ® 1 + df 2 / dr 2 = 1/D2 ® | ||||||||||
| ® (df / dr) 2 = 1/D2 – 1 ® df / dr = [1/D2 – 1]1/2 ® df = [1/D2 – 1]1/2 dr ® f = ∫r [1/D2 – 1]1/2 dr | ||||||||||
|
De este modo podemos obtener una expresión aproximada de la función que representa la curvatura del espacio-tiempo. Nótase que de dicha expresión de deduce un punto crítico en el espacio, que es r = GM/2c2, representado en la ilustración 4 como el punto ‘x’. Esto es así porque es punto en D, y a partir del cual el espacio (f) se hace imaginario (debido a que D < -1). Ese punto crítico, así como el correspondiente al doble de su distancia (es decir GM/c2, donde D se anula), serán tratados a continuación. Bien podríamos decir (salvo que se incorrecta la integración siguiente), que el espacio lineal tiene la forma (f): f = GM/c2 · ln[{ ( GM(2c2r – GM) )1/2 – GM}2 / (c2r – GM)] + 2/c2 · [GM(2c2r – GM)]1/2 Pero, no hace falta usar esta expresión para analizar el espacio, pues simplemente con la expresión de la densidad de espacio y con la ayuda de la relatividad espacial de Einstein podemos hacer un buen estudio del espacio-tiempo. Usemos pues la expresión 7 y la 10. a = 1 + V/ c2 D = 1 + V/ c2 v = ds / dt ® ds = v · dt Sabiendo que el cuerpo debería avanzar siempre en el espacio cuando se encuentra en caída libre, y sabiendo que la velocidad está en función de la posición, así como el paso del tiempo, observamos: a2 / a1= [r1 (r2 c2 – GM)] / [r2 (r1 c2 – GM)] ® a2 = [r1 (r2 c2 - GM)] / [r2 (r1 c2 - GM)] · a1 a2 = (1 - v2 / c2)1/2 ® v2 = c (1 – a22 )1/2 v2 = c (1 – {[r1 (r2 c2 - GM)] / [r2 (r1 c2 - GM)] · a1}2 )1/2 ↔ v2 = c (1 – a22 )1/2 Observemos que si |a2| > 1, v2 toma valor complejo (es decir, no real). En ese caso, ds (el desplazamiento), así como la posición final es también un número complejo. Veamos pues que ocurre para cada posición en la caída libre de un cuerpo, inicialmente casi en reposo (siendo r1 muy lejana a la masa central):
|
||||||||||
|
r2 ® ∞ |
a2 = 1 ó a2 ≈ 1 |
v2 ≈ 0 |
v2 < c |
|||||||
|
r2 ® GM/c2 |
a2 ® +0 |
v2 ® c |
v2 < c |
|||||||
|
r2 = GM/c2 |
a2 = 0 |
v2 = c |
||||||||
|
r2 < GM/c2 |
a2 < 0 |
v2 < c |
|
|||||||
|
r2 ® GM/2c2 |
a2 ® – 1 |
v2 ® 0 |
v2 < c |
|||||||
|
r2 = GM/2c2 |
a2 = – 1 |
v2 = 0 |
v2 < c |
|||||||
|
r2 < GM/2c2 |
a2 < – 1 |
v2 є Complejos |
v2 > 0 |
|||||||
| Ilustración4 | ||||||||||
 |
|
|||||||||
|
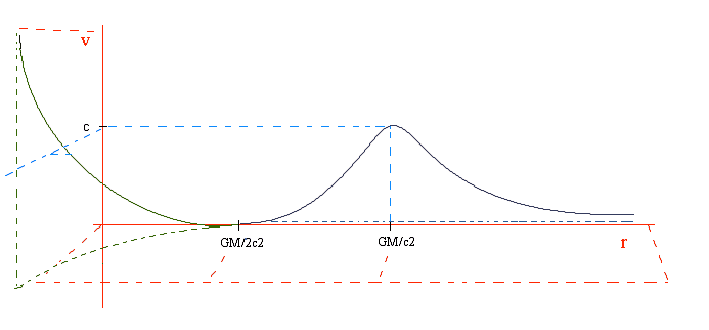
Imagínese el espacio radial (r) en “dos” dimensiones (una real y otra imaginaria), así como también consideraremos la velocidad con valores complejos. El acceso a la dimensión imaginaria se encuentra en el punto r = GM/2c2 a partir del cual, la función de la velocidad (en azul, como real) pasa a tomar valores complejos (en verde) y además, es posible que la velocidad tome, en valor de módulo, valores superiores a ‘c’, claro que eso es en el supuesto que las expresiones obtenidas sean válidas también para esas distancias (menores que r = GM/2c2) o simplemente se traten de meras aproximaciones. El punto r = GM/c2 es tanto el punto donde la velocidad orbital (y de caída) es la de la luz así como también lo es la de escape. Es el punto teórico donde la densidad de espacio (o efectividad) es nula, así como también lo es la velocidad del tiempo. Pero ese punto matemático no tiene porqué tener un referente real (físico) en el espacio, es decir, lo más probable es que no exista como tal, aunque sí las implicaciones referentes a sus inmediaciones. El hecho de que la densidad a partir de dicho punto tome valores negativos y en creciente valor absoluto hace pensar que el espacio se pliega sobre sí por “debajo” de él mismo, y si entendemos el universo como un conjunto de esferas concéntricas temporales (siendo el espacio la superficie de la esfera de cada presente), es posible concebir un viaje al pasado matemático (como se intuía con la expresión de la velocidad del tiempo a esas distancias). Claro está, que para que todo ello pueda darse, la masa central (un agujero negro) debería ser lo suficientemente másico y pequeño como para dejar patentes a gran escala las zonas de efecto retrógrado espaciotemporal; o bien podría bastar con un sistema de grandes masas (estrellas de neutrones, etc.) cuyo potencial suma, en valor absoluto supere el valor c2 en grandes zonas. Este conjunto de posibilidades pueden configurar una teoría del krono”… pero, ¿de verdad podemos admitir la posibilidad de viajar al pasado, o es un espejismo de la imperfecta física de la cual se apoya esta parte teórica? Esta pregunta quedará respondida en la culminación de la teoría de campo gravitoelectromagnético (campo complejo), constituida por la primera y la segunda parte. Relatividad especial a parir de la relatividad general de la fenomenología (volver arriba ↑ ) Durante todo el capítulo hemos alternado la relatividad especial de Einstein con la propuesta de relatividad general de fenomenología. Hemos observado que está en concordancia. Pero, es más, a partir de la aplicación de la energía (o masa) relativista en la expresión general del espacio-masa (11) y con el apoyo directo de la teoría general de la fenomenología, podemos deducir otra vez la contracción de la longitud aparente (impropia) de un cuerpo y la dilatación de su tiempo impropio. ξ = GM/c2 · ln (n/do) (11) l e / l b = l i / l p = D = 1 + V/ c2 (8) Según la relatividad de la fenomenología los efectos producidos sobre el cuerpo son “inversos” a los efectos producidos sobre el espacio, de este modo, si la densidad espacial del espacio disminuye, la densidad espacial del cuerpo aumenta [que es lo mismo que: si la longitud (le) del espacio disminuye, la longitud (ξi) del cuerpo aumenta, puesto que el conjunto es constante], como una relación de causa-efecto. Así pues, sea ‘d’ la densidad espacial del cuerpo, y ‘D’ la del espacio, tenemos que: D = 1/d d = ξi / ξp D = li / lp ξi / ξp = lp / li
m = mo /a Análisis de lo que ocurre cuando aumenta la ‘v’ del cuerpo: Si v ↑ ® a ↓ ® E ↑ Ù m ↑ ® ξ ↑
|
||||||||||
|
ξp = Gmo/c2 · ln (n/do) ξi = Gmo/ac2 · ln (n/do) |
® ξi / ξp = 1/a |
® lp / li = 1/a |
||||||||
|
ξi / ξp = 1/D = lp / li = lp / li |
|
|||||||||
|
Y del mismo modo, podemos deducir la dilatación del tiempo de un cuerpo, aunque resulta más cómodo deducir la expresión por métodos directos, pues según la relatividad general de la fenomenología (y como habíamos dicho anteriormente): “el tiempo es simplemente la inversa conceptual del espacio: El producto de espaciotiempo l·t es constante (para todas las posiciones en el campo gravitatorio), de tal modo que si el uno se dilata, el otro se contrae”. Si consideramos que el campo de velocidades es análogo al como gravitatorio, también tenemos: |
||||||||||
|
lp / li = ti / tp ® tp / ti = a ® tp = ti · a Además, aplicando la hipótesis de la dualidad onda-corpúsculo, podemos llegar a la misma conclusión sin tener que pasar por la relación D = 1/d, pues como l = h / mc, podemos sustituir mo y mo/a en ξp y ξi , respectivamente, por h / lpc y h / lic (para el fotón), y entonces tenemos la relación ξi / ξp = lp / li (para el fotón), de donde se deduce que ξi / ξp = lp / li (para todas las partículas) y como ξi / ξp = 1/a, automáticamente tenemos el resultado: li = lp · a |
||||||||||
|
(volver arriba ↑ ) |
||||||||||
© 2004 ROBERTO MONCHO
_____________________________________________________________________________________________________
A- Espacio-tiempo en el campo gravitatorio (Relatividad General)
B- Fuerza Gravitoelectromagnética (Grelma).
D- Interacción Fuerte-Débil-Grelma (FDG)
|
© 2004 ROBERTO MONCHO |