D- Interacción Fuerte-Débil-Grelma  (IFG)

Nota: Actualmente ete apartado ha sido modificado con la inclusión de una hipótesis más sencilla de la que aquí se expone. En breve estará expuesta. disculpen las molestis. Gracias

    - Introducción.

    - Interacción fuerte-débil.

    - Hipótesis del efecto perturbación real de carga.

    - Ecuación de onda-corpúsculo ligada a un potencial

    - Reconstrucción de la física Grelma a grandes distancias.

INTRODUCCIÓN

En este apartado del trabajo lo que he intentado es reducir, mediante un modelo sencillo la concepción de las interacciones débil y fuerte a la concepción de la Interacción Grelma en un dominio especial (cuando estamos muy cerca de las partículas). No se trata de una teoría unificada a la perfección, sino de una base conceptual muy sencilla que implica la existencia de una única interacción: la Grelma. Para ver ello lo he formalizado como continuación del modelo unidimensional Grelma discontinuo (con “cortes” bruscos en el espacio-tiempo) ya que para matematizar un modelo totalmente continuo (si se puede) sería de un nivel que me sobrepasa.

Interacción fuerte-débil (volver arriba ↑ )

PSETs activados e hipótesis del efecto perturbación real de carga

Definamos el número particular z, de un cuerpo, como un número complejo cuya parte real se corresponde con el número de quarks (H) de la partícula, y la parte imaginaria, que se corresponde con el número leptónico (L). Este número debe conservarse en todas las reacciones (principio de conservación del número particular). Sólo podrán existir aquellas partículas que tengan un número entero en su parte real y en su parte imaginaria (condición de existencia de una partícula). Sea pues:

z = H + L · i

Para entender la identidad de los quarks y los leptones como un mismo tipo de partículas elementales se nos hace necesario definir una estructuración básica común para estos dos grupos. Dicha estructura se considerará subelemental, es decir, sin una identidad individual para los componentes de la estructura total, de forma análoga a como se hizo en su momento a los quarks; este nuevo nivel subelemental lo denominaremos cuartónico o hexa-cuartónico. Dicha estructura la entenderemos, para poder visualizar un orden que nos sea familiar, de forma geométrica (distribución espacial de ligaduras) con una base de 8 elementos derivados de una misma subpartícula: el PSET, representado por la letra a, que tiene un estado real y otro imaginario. Esta partícula tiene antipartícula (ā), y por tanto tendrá cuatro estados de activación (E): +½ , –½ , +⅓i , –⅓i , (los estados positivos se refieren a la partícula y los negativos a la antipartícula). Su número particular será: z = ½E. Si, además, asociamos a cada estado de activación un valor de polarización dual (P = ±½ ), definiremos carga real aportada (Q) por un PSET activado (a^x) como: Q = e · ⅓P. Un PSET no activado se caracterizará por E = 0 y P = 0.

Las partículas derivadas del PSET activado (perturbación) son: a⁺ , a^–, ā^–, ā⁺, a⁺ⁱ , a^–i, ā^–i, ā⁺ⁱ.

Subpart.          E         P      z      Q (e)                         Subpart.             E          P            z      Q (e)

a⁺         +½      +½      +1/4     +1/6                             a⁺ⁱ                 +⅓i         +½           + i/6    + 1/6                   

         a^–         +½      –½      +1/4     – 1/6                             a^–i                  +⅓i         –½           + i/6    – 1/6                    Éstas se asociarán de 6 en 6

ā⁺         –½      +½      – 1/4    + 1/6                             ā⁺ⁱ                 –⅓i         +½           – i/6    + 1/6

ā^–         –½      –½      –1/4     – 1/6                             ā^–i                  –⅓i         –½           – i/6     –1/6

La activación de un PSET tiene lugar por la interacción grelma entre los PSETs energético-imaginarios y los energético-reales, de tal modo que se trata de una traslación constante de la activación (perturbación). La distancia de acoplamiento entre estos PSETs es r_f (6·10^{– 34} m.). Un PSET real (a) se considerará activado (6a*ⁱ) cuando 6 PSETs energético-imaginarios de los alrededores se agolpan a él formando un campo energético-imaginario (es decir, eléctrico) elemental. Un PSET imaginario (aⁱ) se considerará activado (a*) cuando un cierto número de PSETs energético-reales de los alrededores se agolpan a él formando un campo energético-real elemental. De tal modo que los PSETs 6a*ⁱ no tienen masa de campo (aunque sí en su centro), al contrario que las a*, no obstante, en los dos casos, la masa real total en valor absoluto es del orden del fotón en reposo (es decir, despreciable). El campo eléctrico resultante de los acoplamientos entre PSETs activados genera una energía real complementaria a la energía-imaginaria que representa la carga, y además tenemos la energía asociada al propio campo eléctrico secundario (a distancias mayores) que inventa la masa vulgar (la que nosotros asociamos a una partícula libre –de segundo orden-).

Recordemos que tenemos dos dobles estados energéticos, el real (fotón-gravitatón) y el imaginario (carga positivo-negativa). Las partículas a*ⁱ se forman tomando como centro una a de estado real-positivo con los dos estados imaginarios (cargas). En las partículas ā*ⁱ se toma como centro un estado real-negativo. Y en las a*, se ha intercambiado los papeles entre los estados reales y los imaginarios. En todo caso se trata de subpartículas puntuales que integran partículas elementales también puntuales (quarks y leptones) dotados pues de “estructura”.

Definiremos conceptos a partir de los anteriores para entender y simplificar la física:

-          Sea un vector de magnitud, V, sus partes son: V = (valor principal (v1), valor secundario (v2), …) y sus operaciones: V + W = (v1 + w1, v2 + w2, … ); V·W = (v1·w1, v2·w2, … ).

-          Vector elemental de un PSET:                         A = (E, P)                        donde E y P son complejos

-          Supercarga:                                                     M = (z, Q)                       donde z y Q son complejos

-          Número de proporcionalidad elemental:           a = (½, ⅓)

-          Número de estados:                                         S = (±1, ±i)

-          Estados de activación:                                      e = aS

-          Principio fundamental de la física:                  M = S M_i = S a·A_i = constante   

*Partículas de existencia: aquéllas cuya parte principal de la supercarga es entera. Las demás son subpartículas.

*Partículas de primer orden: Partículas de 1ª existencia, es decir, de existencia restringida en el dominio del radio crítico principal (x_o). Serán aquéllas cuya parte real del valor secundario de la supercarga no sea entera.

*Partículas de segundo orden: Partículas de 2ª existencia, es decir, de existencia no restringida en el dominio del radio crítico principal (x_o). Serán aquéllas cuya parte real del valor secundario de la supercarga sea entera.

*Una partícula será la misma que otra si y sólo si tiene la misma supercarga (M).

*La carga absoluta (Q_abs) de una partícula será la suma de los módulos de las cargas parciales (cargas de las subpartículas), excepto en el caso del neutrino, cuya carga absoluta se reduce en un factor k ≈ 0’04 debido a que la carga total se neutraliza dentro del radio de dominio x_o

Part.           Estructura base                    Part.                        Estructura base

u                              4a⁺                                             e^–                                          6a^–i

d                              3a^– + a⁺                                     e⁺                                          6ā⁺ⁱ

ū                              4ā^–                                             n_e-                                        3a^–i+ 3a ⁺ⁱ

đ                              3ā⁺+ ā^–                                      n_e+                                       3ā ^–i+ 3ā  ⁺ⁱ

W⁺                         3ā⁺+ 3a⁺                                      W^–                                        3ā^–+ 3a^–

Z⁰                            6a⁺ⁱ+ 6ā^–i + 6a^–i + 6ā⁺ⁱ             g                                             6a^–i + 6ā⁺ⁱ

g (gluones)?   a⁺ā⁺ā^–a^–;  ā⁺a⁺a^–ā^–; a⁺a^–ā^–ā⁺; a^–a⁺ā⁺ā^–; a⁺ⁱā⁺ⁱā^–ia^–i  ;  ā⁺ⁱa⁺ⁱa^–iā^–i  ; a⁺ⁱa^–iā^–iā⁺ⁱ  ;  ā⁺ⁱā^–ia^–ia⁺ⁱ 

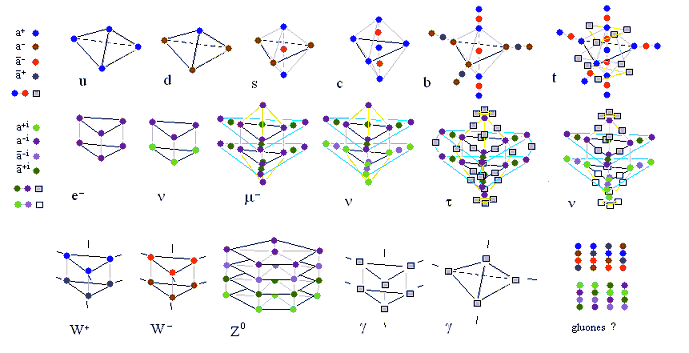Estructura base y complementaria de los quarks y otras partículas. Representación de las cargas absolutas como unidades espaciales.

Las ligaduras (distribución relativa en el espacio) entre las a representan la estructuración más simétrica posible (y, por tanto la más estable). Obsérvese la disposición triangular (de forma análoga a como se predecía para los PSETS) y por tanto, la forma más simple: el tetraedro. Pero luego se va complicando la estructuración al incorporar elementos y en detrimento de la estabilidad de las partículas. Los enlaces abiertos significan que la estructura está inacabada (se debería rellenar de un modo parecido a como se han rellenado los quarks). Los cuadrados en vez de círculos sirven para simplificar la visualización. La estructuración secundaria (complementaria) sigue un determinado orden (muy importante y complejo) que se hace más sencillo si se estudia visualmente: la idea básica es formar una capa intermedia de triángulos sobre la capa base [caso s y c, complementos menos pesados) y luego cubrir los vértices [caso b, algo más pesado] y por último hacer otra capa de triángulos sobre los dos estados anteriores [caso de t, muy pesado]. Para los leptones la complementación se hace directamente a partir del segundo estado (vértices cubiertos y triangulación intermedia, caso m) y luego sigue con la segunda capa de triangulación (caso de t, muy pesado). La partícula Zº se ha representado directamente con estructura secundaria

Reglas de la estructura base de una partícula

1)      El módulo del número particular ha de ser igual a la unidad o igual a cero: ||z|| = 1 ó ||z|| = 0.

2.0) Una subpartícula dominante es aquella que tiene poder para formar partículas sin necesidad de las de carga opuesta y misma z. Dominante es toda aquella subpartícula que [Q·z²] · sign(z) > 0. Esta ruptura de la simetría también se da en la abundancia de las partículas frente a las antipartículas, cumpliendo pues que: Un subpartícula será abundante si Q·z² > 0. Pero realmente no es una verdadera ruptura de la simetría, sino que ésta se ve compartida (dividida) por la dualidad real-complejo en vez de la dualidad partícula-antipartícula o la dualidad de las cargas con un mismo z.

2.1) El ámbito base (B) [el nº de subpartículas de la base, del mismo z, permitido en la estructura base] de las subpartículas recesivas (las que no dominan) es B_rec = ²/_||Q||, mientras que para las subpartículas dominantes B_{dom 1} = ¹/_{|| z ||}  , B_{dom 2} = ¹/_{|| z ||}  – B_rec

3)      La forma de la estructura base se representará buscando la mayor simetría espacial

Reglas de la complementación de las estructuras

1)      El ámbito secundario (S) [el nº de subpartículas de un mismo z, permitidas en una partícula] es S = n·B; donde n es un número natural. En el caso de las partículas con z imaginario, la complementación (y también la formación de la base) tiene lugar con pares de 6a, en vez de con pares de a, pero se representará (en la estructura secundaria como si fuese sólo una a, para simplificar la visualización).

2.1)   Si q_{abs base}< 6    Triangulación intermedia. (Acoplamiento de pares de a formando triángulos con las a anteriores).

2.2)   " q_{abs base}          Cubrimiento de vértices manteniendo los triángulos intermedios (Acoplamiento de las a en los vértices de la figura geométrica).

2.3)   " q_{abs base}          Segunda capa de triángulos (Recubrimiento de toda la base con triángulos).

2.4)   " q_{abs base}               Tercera capa de triángulos [no será necesaria puesto que la masa se dispara].

3)      " q_{abs base}               Cada paso de complementación por el que “ha pasado” una partícula será un grado de completitud (C), [o nº de sabor].

"Principios" de la interacción débil (o desintegración)

1)   Conservación de la Supercarga (M). (Además de conservaciones de momentos).

2)   Mínima energía: Las partículas tenderán a la división en partículas de menor energía (además de tender al mínimo potencial de campo).

3)   Las partículas con el mismo grado de completitud (C) están asociadas (pueden interaccionar entre sí formando un círculo cerrado). [La interacción débil puede explicarse mediante la fuerte (y por tanto la grelma)]

"Principios" de la interacción fuerte

1)   Conservación de la Supercarga (M) y de C (Además de conservaciones de momentos).

2)   Mínima energía: Las partículas tenderán a llegar al estado (potencial) de la mínima energía. [La partículas de primer orden deberán conseguir formar partículas de segundo orden, es decir, formar partículas con carga entera, ya que se reduce la energía residual en dicho caso; y las de segundo orden “buscaran” el punto de potencial mínimo].

3)   Las partículas interaccionan debido a la perturbación real de la carga.

MASA  DE  LOS  QUARKS

Hipótesis del radio crítico dominante (x_o) asociado a los quarks, como propiedad intrínseca del quark genérico.

Todo quark tiene el mismo radio crítico dominante (x_o). Esta distancia cumple la relación: x_o ≈ k Q_abs²/E_real

Suponiendo que x_o≈ 1’9·10 ^–18 m., valor que define la distancia estable entre quarks, y suponiendo que los quarks tienen una estructura base que se rellena por complementariedad [ver dibujo de los quarks] y buscando las simetrías (meta-estables):

Quark        estructura                                             carga abs. (e)                           x_o (m)                              masa (MeV/c²)

u                 4a⁺                                                         2/3                                   4/9 · ke²/m_uc²                                 380 = m_u

d                 3a^– + a⁺                                                                2/3                                    4/9 · ke²/m_dc²                                 380 = m_u

s                 3a^– + a⁺        +  1(ā* + a*)                      1                                       1²  · ke²/m_sc²                                   9/4 · m_u = 850

c                 4a⁺                    +  2(ā* + a*)                      4/3                                   16/9   · ke²/m_bc²                           4 · m_u = 1520

b                 3a^– + a⁺        +  6(ā* + a*)                      8/3                                   64/9  · ke²/m_cc²                             16 · m_u = 6080

t                  4a⁺             + 30(ā* + a*)                     32/3                                 1024/9  · ke²/m_tc²                        256 · m_u = 97280

El símbolo “ * ” denota ambigüedad en el signo de la carga, no obstante, éste ha de ser el más idóneo (que depende de cada situación).  Obsérvese en la ilustración donde se representan los quarks que éstos disponen de una estructura base y una complementaria. La estructura secundaria (que caracteriza a cada quark) puede ser explicada mediante un acoplamiento de la misma polarización del vacío al quark, causado por constituir estados energético-estructurales meta-estables adquiridos por una reacción endoenergética (interacción a altas energías).

MASA  DE  LOS  LEPTONES

Hipótesis del radio crítico dominante (x_o) asociado a los leptones, como propiedad intrínseca del leptón genérico.

Todo leptón tiene el mismo radio crítico dominante (x_o). Esta distancia cumple la relación: x_o ≈ k Q_abs²/E_real

Sea x_o = 2’82 ·10 ^{– 15} m, valor que defininirá el límite de la fuerza eléctrica para electrones. Y sabiendo que la carga absoluta disminuye en un factor k ( ≈ 0’04 ) si la carga total del leptón es cero.

Leptón      estructura                                             carga abs. (e)                 x_o (m)                                   masa (MeV/c²)

e                 6a^–i                                                         1                                       1² · ke²/m_ec²                                    0’512 = m_e

m                 6a^–i                + 7 · (6a*ⁱ + 6ā*ⁱ)            15                                     225   · ke²/m_mc²                             225 · m_e = 115

t                 6a^–i                + 29 · (6a*ⁱ + 6ā*ⁱ)          59                                     3481  · ke²/m_tc²                            3481 · m_e = 1782

n_e               3a^–i +3a⁺ⁱ                                                1·k                                   k² · ke²/m_ec²                                    0’001

n_m               3a^–i +3a⁺ⁱ       + 7 · (6a*ⁱ + 6ā*ⁱ)            15· k                                0’36   · ke²/m_mc²                           0’18

n_t               3a^–i +3a⁺ⁱ       + 26 · (6a*ⁱ + 6ā*ⁱ)          53· k                                4’5  · ke²/m_tc²                                2’3

El valor de k es el de la efectividad de carga absoluta para los neutrinos: Los leptones són más puntuales que los quarks (tienen sus bases más cercas), por consiguiente la carga absoluta es casi la carga total. Suponemos que en los leptones las bases se encuentran un media de ~ (m_u /m_e)^½ ≈ 27 veces más cerca entre sí que en los quarks, en ese caso la efectividad de la carga absoluta disminuirá al sumarse los módulos de las cargas originales a una distancia 27 veces mayor de lo normal, por tanto, cuando la carga total se anule, la carga absoluta será:

Q_{abs efectiva} = Q_{abs real} · sin(1/27)                   →                  k = sin(1/27) ≈ 0’04

Si le damos la vuelta a la explicación, diremos que: La efectividad de la carga absoluta para los neutrinos (k) es, al estar intrínsicamente subordinados el mismo espacio-tiempo, equivalente a la densidad relativa del vacío (k = 0'034), con lo que obtenemos un factor 29 entre las distancias relativas entre las bases de los neutrinos (leptones neutros) y los quarks.

La diferencia entre las masas m_u y m_e puede deberse a la diferencia entre los tiempos de acoplamiento que tienen lugar en la formación de las bases leptónicas (t) y quarkónicas (t), siendo x_e/x_u = m_u /m_e ≈ ⅔(2pb), donde b = (t /t) ^1/2 es el factor de acoplamiento de la carga, el ⅔ se debe a que los quarks se componen de 4a* mientras que los leptones de 6aⁱ*, es decir |4a*/6aⁱ*| = ⅔ y el 2p viene por la relación geométrica (los leptones son puntos lineales, mientras que los quarks son puntos circuloides).

Hipótesis del efecto perturbación real de carga (volver arriba ↑ )

El campo eléctrico presenta un origen espacial en lo que denominamos radio crítico dominante (x_o). Por debajo de éste se encuentra la perturbación energético-real complementaria a la carga, es decir, una densidad energética negativa, que consideraremos constante entre dos radios críticos (que serán x_r y x_o). Pues bien, el efecto de fuerza de dicha perturbación de ve reducida por pliegues del mismo espacio-tiempo (e-t) cerca del círculo central de la perturbación (con radio, con un factor n, el radio crítico medio [o total] x_q), en proporción al radio crítico dominante (x_o): es decir, encontraremos una reducción directamente proporcional al círculo 2pnx_q e inversamente proporcional a x_o. Por tanto, consideraremos la posibilidad de que la Interacción Fuerte (IF) se deba a dicha perturbación energética. Por otro lado descartaríamos la existencia de la carga de color (ya que no se nos hace necesaria) a favor de la carga absoluta que haría su papel conjuntamente con el número z que describe a la partícula.

Por el principio de equivalencia entre carga y masa, sabemos que la energía real de una carga es:

E_q = (k/G)^½ · Q_{real abs} ·c²

Pues, su complementaria, debería ser la energía de la autofuerza de la IF sin reducir: (energía fuerte: E_f):

E_f = – (k/G)^½ · Q_{real abs} ·c²

Los quarks y leptones son las partículas a las que podríamos considerar elementales (pero teniendo en cuenta su valor absoluto como cuartos y hexa-cuartos), por tanto, la interacción fuerte (IF) que se deduce a partir de la hipótesis anterior debería funcionar para estas partículas (Teniendo en cuenta que los leptones se salvan en cierta parte de la IF). Además, nos hace falta otra hipótesis: La densidad de energía se encuentra prácticamente toda en el “pozo crítico”, y sin embargo existe un residuo que decrece en proporción al cuadrado de la distancia relativa a x_o (ya que se distribuye en un plano con agujero el círculo de x_o) hasta una distancia límite que viene dada por el tiempo cuántico (t) de la partícula central. Veremos todo eso después de recopilar conceptos:

Conceptos:

Carga imaginaria (Q_im)                                              Q_im = (G/k)^½ M_real

         Módulo de la carga asociada a una masa.

Carga compleja (Q)                                                   Q = Q_real + i·Q_im                                         Q = åq_i

         Carga real + carga imaginaria

Carga absoluta (Q_abs)                                                Q_abs = å||q_i||

         Suma de las cargas, en módulo, que forman la partícula           Q_abs(–⅓e) = ⅔e                –⅓·e = (–¹/₆ –¹/₆ –¹/₆ + ¹/₆)e

                                                                                  Q_abs(⅔e)  = ⅔e                 ⅔·e = (¹/₆  + ¹/₆  + ¹/₆  + ¹/₆)e

                                                                                                              Q_abs(prot.)  = 2·e             1e = (⅔ + ⅔ – ⅓)e

                                                                                                              Q_abs(neut.) = 2·e             0 = (⅓ – ⅓ – ⅓)e

Signo de carga (u_q)                                                   u_q = Q/Q_abs                                      u_q12 = u_q1 · u_q2

         Relación carga compleja / carga absoluta             

Número fuerte (n)                                                      n = 1 + z²

              Número asociado a las partículas de la IF

Tiempo fuerte (t_f)                                                       t_f = h/M_rc²

              Tiempo cuántico de un quark de masa M_r

RADIOS:

Radio crítico dominante o principal (x_o)                 x_o = k Q_abs²/E_real                                                                                             = 2·10 ^–18 m

              Radio-origen del subcampo dominante (del grelma)

Radio crítico reducido (x_r)                                        x_r = k Q_im²/E_real            →               x_r = GM_r/c²                  

              Radio-origen del subcampo gravitatorio

Radio crítico total (x_q)                                               x_q = k Q_abs²/||E_total||        →               x_q ≈ (Gk)^½ Q_abs/c²

              Radio-origen de la perturbación total

Radio fuerte (x_f)                                                         x_f = t_f·c                          →               x_f = h/M_rc              = 4·10 ^–15 m

              Radio de alcance de la interacción fuerte

Pozo crítico (Pz)                                                         Intervalo comprendido entre (x_o, x_r)

Densidad de espacio (D)                                         D = 1 + V/c² = 1 – GM_r/rc²

         Cociente: espacio efectivo / espacio base

Longitud de pliegue (p)                                           p = r·(1 – D) = GM_r/c² = x_r

         Espacio que se “pierde” por el pliegue del e-t

Círculo crítico total plegado (c_p)                             c_p = 2pn(x_rx_o)^½ = 2pnx_q

         2pn·Media geométrica entre la long. de pliegue y el radio crítico = 2pn·Radio crítico total

DOMINIO1: [x_r, x_O]

Reducción crítica (C_c)                                                                  C_c = c_p/x_o = 2pn(x_r/x_o)^½

         Efecto de contracción de magnitudes en el Pz

Densidad lineal de energía crítica (J)                                       J = E_f/(x_o – x_r)                J ≈ E_f/x_o                   

         Energía fuerte distribuida en el Pz  

DOMINIO2: [x_O , x_f]

Reducción crítica residual (C_c’)                                                C_c’ = c_p/r = 2pn(x_r/r)^½

         Efecto de contracción de magnitudes hasta r

Densidad lineal de energía residual (J’)                                 J’ ≈ [x_o²/r²] · J               J’ ≈ x_oE_f/r²             

         Energía fuerte distribuida hasta r

         [Sabiendo que es proporcional al cuadrado del cociente de x_o y r

Autofuerza Grelma [y_g]                                            [y_g] = k Q_abs²/r²                  " r Î (x_o , n)

Interacción Grelma |IGñ                                             |IGñ = [y_g]₁^½ [y_g]₂^½ · u_q12 ·|u_rñ

                                                                                     |IGñ = k q₁q₂/r² · |u_rñ          " r Î (x_o , n)

DOMINIO: [x_r, x_O]

Autofuerza Fuerte [y_f]                                             [y_f] = – C_cJ                       " r Î (x_r , x_o)

Interacción fuerte |IFñ                                               |IFñ = [y_f]₁^½ [y_f]₂^½ · |u_rñ   

                                                                                     " r Î (x, n)

                   [y_f] = – C_c · (k/G)^½ · Q_abs. ·c² /x_o ]

                   [y_f] = – 2pn· (x_r/x_o)^½(k/G)^½ · Q_abs ·c² /x_o = – 2pn · (KM_r)^½ · Q_abs ·c /x_o^3/2

_{{x, n}}ò[y_g]_electr dr = E_{real                           {x, n}}ò[y_g]_gravit dr =  – E_real                             òCarga = i · E_q                 ò[y_f]dr = – E_q        

ò_total [y_f]dr = – ò_dominio1 J dr  – ò_dominio2 J’dr = – _aproxE_q – _aprox0 ≈ – E_q

ò_reducida [y_f]dr ≈ – C_c·E_q = – 2p M_rc²          Energía fuerte resultante inducida por la carga

Análisis de la Interacción Fuerte-Grelma (IFG) para el enlace up-down:

q₁ = 2/3 · e          q₂ = 1/3 · e

z₁ = z₂ = 1            n =2                           x_o1= 4/9 · ke²/M_rc²                    x_o2= 4/9 · ke²/M_rc²                    x_o= 4/9 · ke²/M_rc²

IG(r = x_o) = 2/9 · ke²/x_o²                        IF(r = x_o) =  –  4p· (kM_r)^½ · 2/3 ·e ·c /x_o^3/2                                = – 4’5 ·10⁸ N

| IF / IG | = 8/3·p· e²/(q₁q₂) · [(x_oM_rc²)/(ke²)]^½ = 8/3·p· (9/2) · 2/3 = 25’1 = F_A

Análisis de la Interacción Fuerte-Grelma (IFG) para el enlace up-up:

q₁ = 2/3 · e          q₂ = 2/3 · e

z₁ = z₂ = 1            n =2                           x_o1= 4/9 · ke²/M_rc²                    x_o2= 4/9 · ke²/M_rc²                    x_o= 4/9 · ke²/M_rc²

IG(r = x_o) = 4/9 · ke²/x_o²                        IF(r = x_o) =  –  4p· (kM_r)^½ · 2/3 ·e ·c /x_o^3/2

| IF / IG | = 8/3·p· e²/(q₁q₂) · [(x_oM_rc²)/(ke²)]^½ = 8/3·p· (9/4) · 2/3 = 12’6 = F_B

Análisis de la Interacción Fuerte-Grelma (IFG) para el enlace down-down:

q₁ = 1/3 · e          q₂ = 1/3 · e

z₁ = z₂ = 1            n =2                           x_o1= 4/9 · ke²/M_rc²                    x_o2= 4/9 · ke²/M_rc²                    x_o= 4/9 · ke²/M_rc²

IG(r = x_o) = 1/9 · ke²/x_o²                        IF(r = x_o) =  –  4p· (kM_r)^½ · 2/3 ·e ·c /x_o^3/2

| IF / IG | = 8/3·p· e²/(q₁q₂) · [(x_oM_rc²)/(ke²)]^½ = 8/3·p· (9/1) · 2/3 = 50’3 = F_C

Análisis de la Interacción Fuerte-Grelma (IFG) como una media geométrica de los 3 pares:

| IF / IG | = (F_A F_B F_C)^1/3 = 25’1

Análisis de la Interacción Fuerte-Grelma (IFG) para dos protones:

DOMINIO: [x_O, r]

                   [y_f] = – C_c’ · (k/G)^½ · Q_abs. ·c² x_o /r² ]

                   [y_f] = – 2pn(x_r/r)^½ (k/G)^½ · Q_absc² x_o /r² = – 2pn(Kx_r/G)^½ · Q_absc² x_o /r^3/2 = – 2pn(KM_r)^½ · Q_absc x_o /r^5/2

r = 10^{– 15} m                                             Q_abs = 2e                             n = 10

| IF / IG | = 40px_oc(M_r/rk)^½ · 1/e = 19’7

Análisis de la Interacción Débil-Fuerte-Grelma (IDFG) para up-down:

La interacción débil puede explicarse a partir de la interacción fuerte entre partículas de z = 0 y de z ¹ 0. Realmente lo que ocurre es que se “busca” dividir las partículas en otras de menor energía, creando pasos intermedios (partículas con z = 0) entre estos dos estados (donde z_inicial = z_final). Esas partículas intermedias son las W y Z, que existen virtualmente en el espacio (como todas las demás) esperando a “activarse” con la energía-carga que le pueda ceder una partícula de z ¹ 0, de tal modo que es un juego de “probabilidades” (cuanto mayor sea la energía de la partícula inicial, tanto mayor será dicha “probabilidad” de cesión), por tanto, se trata de una interacción entre la partícula inicial y el espacio que le rodea (lleno de partículas a inactivadas). Una vez W/Z a ganado la energía suficiente, sólo ha de dividirse en dos partículas de menor energía de estructura (normalmente C_final = C_inicial – 1 ). Esta interacción será pues simplemente una consecuencia del principio de mínimos y no presenta un campo de fuerzas distinto al fuerte-grelma, por tanto es un fenómeno regido por las mismas leyes que las demás interacciones (fuerte-grelma) y no debería pues constituir como una fuerza independiente. Así mismo, ahora la estudiaremos brevemente haciendo su tratado como un caso particular de la interacción fuerte:

Consideraremos que existen las partículas W/Z preactivadas (con estructura base pero sin masa) y que, por tanto, interaccionarán con las partículas inestables, según las expresiones de la IF para el dominio mínimo (d ≤ x_o)

Interacción entre W⁺ y W⁺

z_w = 0                                                                      x_o= ke²/M_wc²

n = 1                                                     

F = – 2pn · (KM_w)^½ · Q_abs ·c /x_o^3/2

F = – 2p · (KM_wc²)^½ · e·/(M_rc²/ke²)^3/2 = – 2p (M_wc²)² / ke²                                        |F₁| = 4’48·10¹² N

Interacción entre u⁺ y W⁺

z_w = 0 ;  z_u = 1                                        x_w = 1² · ke²/M_wc²                     x_u = 4/9 · ke²/M_ec²                   x_o= 2/3 · ke²/M_rc²

n_u = 2;    n_w = 1                                     n = (n_wn_u)^1/2                       M_r = (M_wM_u)^1/2                          Q_abs = (Q_wQ_u)^1/2

F = – 2pn · (kM_r)^½ · Q_abs ·c /x_o^3/2

F = – 2p ·2^½ · (kM_rc²)^½ · 2/3· e· (3M_rc²/2ke²)^3/2  = – 2p · 1/3^½ · e·(M_rc²) ²/ke³   = – 2p ·1/3^½ · (M_rc²)² / ke²

F = – 2√3 · p · GM_r²/ke² · c⁴/G                                                  a = 2p ke²/h

F₂ = – 4√3 · p² · GM_r²/ha · c⁴/G

                                            F_x = – (n_xe/Q_x)^½  · M_x/M_w · |F₁|

F₂ = – √3 · M_u/M_w · |F₁| = – 3’2 ·10¹⁰ N

Interacción entre ½ m⁺ y W⁺ (sólo interacciona la mitad del m⁺ , es decir, 45a )

z_x = i/2                 n_x = 3/4                                 Q_x = 15/2

F_x = – (n_xe/Q_x)^½  · M_a/M_w · |F₁|

F₃ = – 1/(10)^½  · M_x/M_w · |F₁|

Pero si suponemos que la interacción débil no tiene lugar en las distancias del orden de d = x_o sino mayores, entonces, según la expresión de la IF para ese dominio, debemos corregir la expresión final como:

                                            F_x = – (n_xe/Q_x)^½  · M_x/M_w · |F₁| · x_o /r

Y como podemos intuir que r será de alrededor de 100 veces x_o entonces, la fuerza de las desintegraciones será del orden de 10⁸ N.                                           

Equación de onda-corpúsculo ligada a un potencial (volver arriba ↑ )

En el marco de esta base teórica, las partículas son realmente perturbaciones de espacio, así mismo, la masa-carga (aparatado de fuerza compleja) quedaba representada por la “autofuerza primaria” [y’], que generaba la energía que la define. Si bien, en la perfección de la base teórica (este apartado), quien genera la energía real de una partícula es el campo electromagnético asociado a la carga absoluta intrínseca. A este campo de perturbación lo denominaremos autofuerza eléctrica [y_e]

[y’]     = GMm_s/r²       r Π [d_o , n]       autofuerza primaria                d_o = Gm_s/c²

U’ = ∫[y’] dr = Mc²

[y_e]     = k Q_abs²/r²      r Π [x_o , n]       autofuerza primaria                x_o = k Q_abs²/E_real

U = ∫[y_e] dr = Mc²

Recordemos que la autofuerza primaria surgió como campo complementario a la autofuerza secundaria, y ahora sabemos que el origen de dicho campo primario recae en la perturbación que genera la carga absoluta de la partícula.

De cualquier modo el potencial asociado (U) se corresponde con la energía de la partícula. Así pues, si consideramos un potencial relativamente estático, la energía que generaría sería la del reposo de una partícula. Esto es:

U = ∫[y_e]_o dr = M_oc²

Y con esto, hemos obtenido una ecuación muy sencilla que relaciona el potencial de la perturbación (o onda electromagnética generalizada) con la partícula asociada (o fotón generalizado). Supondremos, pues, que dicha relación se cumplirá para toda onda-corpúsculo asociada a un potencial energético (U) relativamente estático (con desplazamiento lento respecto al sistema de referencia):

U = E_o                       Y por tanto:

– E_o + U = 0

Esta sencilla relación no nos informa sobra las caracteríticas de la onda asociadad a la partícula dentro del potencial U, y por eso vamos a incorporar nuevos términos, pero siempre manteniendo la igualdad:

Sumamos a los dos términos la energía total de la partícula (E), por supuesto, relativista:

E – E_o + U = E                        E = hn = mc² = gm_oc²                                    g = (1 – u² /c²) ^{– ½}  

Observemos que E – E_o es la energía cinética (E_c) de la partícula:

E_c + U = E

Multiplicamos los dos términos por la ecuación general de onda e.m. Y = Y_oe ^{i (2p x / l  –  wt)} , donde las dimensiones (analíticas) de dicha onda vendrán dadas a nuestro gusto (bien distancias, bien elongación relativa, etc.):

(E – E_o)·Y + U·Y = E·Y

Ahora observemos las propiedades de la onda generalizada:

Y = – (2p /l)² · dY ²/dx² 

Y =  – 1/w i · dY/dt =  i /w · dY/dt

Substituiremos algunos términos por su expresión equivalente de tal modo que obtengamos una equación diferencial que luego generalizaremos (debido al comportamiento de ondacorpusculra de la luz) a cualquier partícula encerrada en un potencial U:

– (l /2p)² · (E – E_o) · dY ²/dx²  + U·Y = i /w · E · dY/dt

Hemos obtenido una ecuación diferencial que, como hemos dicho, y según el marco de esta teoría, podemos generalizar el comportamiento de la luz a toda partícula veloz afectada por un potencial U. Pero antes de ello haremos que la expresión no dependa de las características l y w, de tal modo que ya podremos generalizar. Aplicando las definiciones de energía total de la partícula (E):

 E = hn = ħw                  E²  = p²c²  + E_o²                                                                Donde    p = gm_ov                    E_o = m_oc²                                   

                                      E² –  E_o² = p²c²                                                                            

                                  (E  –  E_o) (E  +  E_o)  = p²c²

                                  (E  –  E_o) = p²c² / (E  +  E_o)

l = h/p    →   lp = h      (De Broglie)

– (l /2p)² · (E – E_o) · dY ²/dx²  + U·Y = i /w · E · dY/dt

– (l /2p)² · p²c² / (E  +  E_o) · dY ²/dx²  + U·Y = i /w ·  ħw · dY/dt

– (lp /2p)² · c² / (E  +  E_o) · dY ²/dx²  + U·Y = i·ħ · dY/dt

– (h /2p)² · c² / (E  +  E_o) · dY ²/dx²  + U·Y = i·ħ · dY/dt

– ħ² · c² / (E  +  E_o) · dY ²/dx²  + U·Y = i·ħ · dY/dt

 – ħ² · c² / (E  +  E_o) · dY ²/dx²  + U·Y = i·ħ · dY/dt

Ahora la expresión obtenida ya no depende explícitamente de la longitud de onda (l) ni de la velocidad anugular (w) y ya se trata de una ecuación general, aunque sólo para una dimensión. Pero, como era de esperara, si realizamos una aproximación para partículas poco veloces en comparación a la luz (por ejemplo, los electrones), la expresión se puede simplificar más:

E  +  E_o =   mc²  + m_oc²  =   (m  + m_o)c²  ≈ 2m_oc²  ≈ 2mc²

Así pues:

– ħ² · c² / (2mc²) · dY ²/dx²  + U·Y = i·ħ · dY/dt

– ħ²/2m · dY ²/dx²  + U·Y = i·ħ · dY/dt

Con la aproximación, curiosamente obtenemos la ecuación de Schrödinger, que, a partir de ahora la consideraremos como una ecuación no relativista del fotón generalizado (u onda-corpúsculo), que sólo será válida para partículas lentas.

En general, deberíamos utilizar la siguiente: 

– ħ²/jm_o · dY ²/dx²  + U·Y = i·ħ · dY/dt                               j = ( 1 + g )

Y, para el fotón, la ecuación quedaría como:

 – ħ²c²/E · dY ²/dx²  + U·Y = i·ħ · dY/dt

Evidentemente, cuando asociamos una onda a una partícula, nos referimos al nuevo concepto de onda: perturbación de espacio concebida como distribuciones no-homogéneas de la densidad de espacio. Con este concepto, la función de ondas (Y) se corresponde pues con un indicador de la densidad de espacio de dicha perturbación total, y por tanto, nos estará informando sobre la contención parcial de la partícula en un espacio dado, ya que ahora la partícula ya no se encontraría localizada en un único punto, sino que su energía (es decir, la partícula) estará distribuida por toda la perturbación que representa, a modo de una distribución de 'probabilidad'. "La probabilidad de encontrar una partícula" no es el concepto más adecuado para emplear en este marco teórico sino, más bien el siguiente:

Coeficiente de determinación: valor del 0 a 1 que nos indica la contención, en un espacio determinado, de la partícula. Es decir, es el valor de la contención o determinación parcial.

Si nos fijamos en la función de onda Y para una partícula, ésta ha de estar distribuida en todo el universo, y por tanto, la distribución (o contención) total debería ser la unidad:

||Y||_universo = 1

El módulo de la función de onda (o perturbación) puede definirse como la media geométrica vectorial de la función y su conjugado; por tanto:

||Y||  =  (Y×Y*) ^½

1²  = ||Y||²  =  Y × Y* = ∫ Y·Y* dr           límites de integración: (– n,  n) ,  donde n es el radio del universo

De este modo, la distribución máxima (1) queda definida como el area, del cuadrado del módulo de la función, para todo el dominio. Y, podemos generalizar la definición para cualquier distribución parcial, tomando los límites de integración adecuados. Si bien, también podríamos escoger la raiz cadrada de esa valor para definir la distribución, pero por razones matemáticas, elegiremos la definición cuadrática ya que proporciona únicamente valores reales y positivos.

Con la ecuación general de onda corpúsculo podemos estudiar el comportamiento de cualquier partícula ligada a un potencial energético U. Desde un punto de vista abstracto, podemos imaginarnos el universo como un sistema ligado a un potencial energético de expansión, generado por una autofuerza primaria [y’]:

[y’] = GM_um_s/R²                      M_u = masa del universo         n = R = radio del universo = T·c         c = vel. expasión = vel. luz

U = [y’]·R = GM_um_s/Tc

j = ( 1 + g ) = ∞

Y = supuesta elongación asociada, perpendicular a la expansión del universo:

 – ħ²/jm_o · dY ²/dx²  + U·Y = i·ħ · dY/dT                    El coeficiente de la “parcial segunda respecto a x” es cero:

 U·Y = i·ħ · dY/dT          Ecuación de la elongación del universo en su expansión

 Y = Y_oe ^{i ( U/ħ · T )}               Y = Y_oe ^{i 2p ( U/h · T )}           Solución de la ecuación.

GM_u/c = n·c = Tc²

m_s= h /Tc²                 

U = GM_um_s/Tc = h/T                     Y = Y_oe ^{i 2p ( [h/T]/h · T )} = Y_oe ^{i 2p ( 1 )} = Y_o

Por consiguiente concluimos que el universo, en su expansión, no sufre ningún comportamiento ondulatorio, cosa que era de esperar ya que la expansión ha de ser totalmente rectilinea y en la dirección del tiempo (la expansión del universo es igual al transcurso del tiempo, lo cual hace que no quepa lugar movimientos de “vaivienes”).

Reconstrucción de la física grelma a grandes distancias. (volver arriba ↑ )

Si cogemos las definiciones de los radios críticos para distancias grandes a las partículas (o a los cuerpos complejos), podemos simplificar en número las expresiones: utilizaremos aquellas que den origen a las interacciones de largo alcance para definir la física grelma a grandes distancias.

Cuerpo de números complejos

Recordemos que el espacio se comporta como energía (o viceversa) y que podemos asignar una correspondencia entre carga i energía haciendo uso de los números complejos, de tal modo que la Ley de la electrostática de Coulomb y la de la gravitación de Newton se convierten en la misma expresión. Por todo ello, podemos unificar algunos de los principios de conservación: sea pues el del momentoenergía y el de la carga, a favor de la conservación de la energía (o su correspondiente espacio).

Principio fundamental de la física grelma:

Conservación la energía total [al menos durante un diferencial de edad del universo] (y por tanto también del espacio efectivo total, que implica la conservación de la supercarga): (Principio 1)

∆E_k = 0

∆E _k = suma de las variaciones de E de tipo k (espacio-masa, espacio-efectivo-accesible, espacio-carga, etc.)

Conociendo las expresiones siguientes: límite de los acontecimientos real (x) y el complejo (c), relación masa-carga (m_q), masa-espacio (ξ), masa de un PSET (m_s) y su energía (e_s), etc.

c = GM/c²                                                                                       c_o = GM_o/c²                                                                                      x = |c| = G|M|/c²              

e_s = m_s c²                                                                   E = Mc²                                                                                               E_o = M_oc²

m_q = – (k/G)^1/2 · q · i   (Principio 2)                           e_q = – (k/G)^1/2 · q · c² · i                                              ξ µ M

Ley de interacción de las energías

Definamos primero las autofuerzas para cuerpos puntuales:

Autofuerza primaria [y’]              = campo de energía definido entre el punto (PSET) de posición y el límite de los acontecimientos, x.

                                                                                  [y’] = ce_s /r²

                                                                                                                           [y’] = (GM/c²)(m_sc² ) /r² = GMm_s/r²

Autofuerza secundaria [y ]            = campo de energía definido entre el límite de los acontecimientos, x, y el resto del universo.

                                                                                  [y ] = – cE /r²

                                                                                                                           [y ] = (GM/c²)(Mc² ) /r² = – GM²/r²

Autofuerza secund. mínima [y_o]    = autofuerza secundaria asociada a una energía de reposo. Autofuerza de reposo:

                                                                                  [y_o] = – c_oE _o /r²

                                                                                                                           [y_o] = (GM_o /c²)(M_oc² ) /r² = – GM_o²/r²

Definamos ahora la transformación grelma:

Transformación general, T_ij        = Operador-factor de transformación entre un campo (o magnitud) estático (central) y uno dinámico:

                                                                                  T_ij = { 1 + 1/c² · [ |v_iñ ´ ( |v_jñ  ´ )]} ·

                                                                                  Ejemplo:    T₁₂ |u_rñ = { |u_rñ + [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ )] /c²}

Definición de la media geométrica de las autofuerzas:

                                                      [f ]  = media geométrica entre las autofuerzas de dos campos (o cuerpos):

                                                                            [f₁₂] = [y₁]^½[y₂]^½                                                                                                                         

                                                                                  [y]^½ = k^½ ·Q/r  = G^½ ·M/r ·i

LEY  DE  INTERACCIÓN  DE  LAS  ENERGÍAS

Toda energía realiza una interacción, |F₁₂ñ, a otra que viene definida por la transformación grelma de la media geométrica de las autofuerzas de dichas energías (o masas complejas), aplicada en la dirección del vector posición, |u₁₂ñ. (Principio 3)

                                         |F₁₂ñ = [f₁₂] T₁₂·|u₁₂ñ

                                                                                                              |F₂₁ñ = – GMm/r²  ·  { |u_rñ + [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ  )] /c²}

A esta interacción la llamaremos: fuerza grelma (fuerza gravitoelectromagnética)

En el caso de tratarse de energías con reposo relativo (sea la masa central, la referencia de coordenadas, o bien sean masas imaginarias en reposo), la transformación T₁₂ es igual a 1, y por tanto la interacción q se desprende es:

                      |F₁₂ñ = [f₁₂]·|u₁₂ñ                      |F₁₂ñ = – GM_om/r² = kQq/r²               [aplicando la correspondencia entre masa y carga]

De esa forma se deduce la gravitación ralativista (la masa gravitatoria, m, es igual a la masa inercial) y la electroestática clásica.

Si aplicamos la fuerza grelma para 2 masas imaginarias (cargas), obtenemos la ley de Lorentz, y de ella se puede deducir la ley de Biot y Savat, la ley de Gauss, etc. :

|F₂₁ñ = – GMm/r²  ·  { |u_rñ + [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ  )] /c²}  = kQq/r²  ·  { |u_rñ + [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ  )] /c²}  Lorentz

|F₂₁ñ = kQq/r²  ·  { |u_rñ + [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ  )] /c²} =  kQq/r²  · |u_rñ   + k/c² ·Qq/r² [ |v₂ñ ´ ( |v₁ñ  ´ |u_rñ  )] =

         =  kQq/r²  · |u_rñ   + q·|v₂ñ ´ (k/c² Q/r² · |v₁ñ  ´ |u_rñ  ) = kQq/r²  · |u_rñ   + q·|v₂ñ ´ (m/2p ·Q/r² · |v₁ñ  ´ |u_rñ  ) =

         = kQq/r²  · |u_rñ   + q·|v₂ñ ´ |B₁ñ  = |F_electrñ + |F_magnñ = campo central + campo no conservativo

|F_electrñ = kQq/r²  · |u_rñ  = q·|Eñ                                      |Eñ = 1/4pe_o · Q/r²                        Siempre podemos definir nuevas constantes

|Eñ = 1/4pr²  · Q/e_o        para una partícula con carga

|Eñ = 1/S  · Q/e_o                                                                                              

|Eñ · S = Q/eo                         Generalización :

Ley de Gauss:

|Eñ = – Ñ· F                                                                   F = kQ/r                                                   Ñ =  d /dr · |u_rñ

Transformaciones que derivan de la general

Definamos:

Autoposición |u_oñ = cualquier vector unitario perpendicular a la dirección de una partícula. Por ejemplo:

                                                         |u_oñ = lim [(0, r +dr, 0)  – (0,  r,  0) ]/dr                      dr → 0

                                                                                                                                              |vñ = (v, 0, 0)

Transformación de la masa-energía ( 1/a ):

La transformación general grelma (T_ij) también debería ser válida para una partícula individual, de tal modo que su autofuerza resultante [y_T]de la transformación debería ser igual a la autofuerza de reposo [y_o], ya que consideraremos la autofuerza total invariable (conservación de la energía)

Consideremos una partícula con una dirección y un sentido en el espacio, es decir, una velocidad |v₁ñ, y con una posición relativa a sí misma, de vector unitario la autoposición. La transformación resultante de la autofuerza [y ] es:

[y_T] = [y_o] = [y ] · áu_o| T₁₁|u_oñ                               puesto que las autofuerzas son magnitudes escalares (no vectoriales)

[y_o] = [y ] · ( áu_o|u_oñ + áu_o| [ |v₁ñ ´ ( |v₁ñ  ´ |u₀ñ )] /c² )

[y_o] = [y ] · ( 1 – v₁²/c² )                                        =                          – GM_o²/r²  = – GM²/r² · ( 1 – v₁²/c² )

M_o²  = M² · ( 1 – v₁²/c² )       →  M_o = M · ( 1 – v₁²/c² ) ^1/2

M = M_o / ( 1 – v₁²/c² ) ^½                                                                             a = ( 1 – v₁²/c² ) ^½

M = M_o / a                                           (E = m c²)                     E = E_o / a

Esta es expresión de la transformación de la masa-energía desde un reposo a una cinética. Así pues, la variación entre la energía de reposo y la final (de la transformación), se corresponderá a la energía asociada al movimiento, a la que llamaremos energía cinética (E_c):

E_c = ∆E = E – E_o = m_oc² /(1 – 1/a)

La energía potencial gravitatoria (E_p) se deduce directamente de la parte conservativa de la interacción general de las energías: E_p =  – GM_om/r

A la suma de las energías cinética y potencial la llamaremos energía mecánica (E_m). Pues bien, aplicando la ley fundamental de la física grelma (conservación de la energía) obtenemos la expresión de la variación de la frecuencia de un fotón en el campo gravitatorio (efecto “Doppler” gravitacional) utilizando m = hn/c². estudiando de cerca este fenómeno, podemos encontrar la fórmula de la densidad de espacio ( D = 1 + V/c² , donde V =  – GM/r ) , y con ella deducir la relación entre espacio “desplazado” y masa (correspondencia masa-espacio, ξ = c · ln (n /c), donde c = GM/c²). Debido al principio de conservación del espacio-energía, se deduce que la relación entre las longitudes impropia y propia , ξ _i /ξ _p = 1/D, y aplicando la conservación de la energía en un campo gravitatorio, sabemos que a = D, con lo que tenemos que l _i / l _p = ξ _p /ξ _i = a, y por tanto, también que t _i /t _p = 1/a , con lo que obtenemos la teoría especial de la relatividad de A. Einstein: velocidad límite, transformaciones de Lorentz, etc. Con todo esto ya podemos obtener prácticamente toda la mecánica y electromagnetismo. (volver arriba ↑ )

© 2004 ROBERTO MONCHO

_____________________________________________________________________________________________________